Cuotas y probabilidades de la ruleta

El juego de la ruleta atrae a millones de jugadores con la promesa de ganancias rápidas y fáciles si tan solo su número de la suerte apareciera en el próximo lanzamiento de la bola. Las reglas de la ruleta son fáciles de dominar, pero muchos jugadores sin experiencia no reconocen el hecho común de que cuanto más simple es un juego de casino, mayor es la ventaja que tiene la casa sobre quienes lo juegan. Lo mismo se aplica con toda su fuerza al atractivo juego de azar que es la ruleta.

Es posible que el juego no requiera que los jugadores sean genios matemáticos, pero sería imposible para ellos emerger como ganadores a largo plazo sin ganar una comprensión adecuada de conceptos como probabilidades y probabilidades. Si bien no existe una forma segura para que un jugador de ruleta haga una predicción correcta sobre qué número acertaría en el próximo giro, tener al menos una comprensión básica de las probabilidades y la probabilidad puede ayudarlo a tomar decisiones mejor informadas sobre qué tipos de apuestas para colocar. Si es nuevo en este emocionante juego de azar, siga leyendo para obtener una breve introducción sobre cómo se aplican los conceptos de probabilidades y probabilidades a la ruleta.

El concepto de probabilidad en la ruleta

Antes de poner en riesgo sus propios fondos y realizar sus primeras apuestas con dinero real en la ruleta , debe obtener al menos una comprensión básica de lo que significa probabilidad. En términos generales, este término se usa para indicar la probabilidad de que ocurra un evento aleatorio dado. Dicha probabilidad se expresa en forma de fracciones o como porcentaje.

La probabilidad de que ocurra un evento aleatorio se puede mostrar en una línea y se le asigna un valor que varía entre 0 y 1 como 0 ______ 1 / 2______1. En el lado izquierdo, tenemos 0, lo que significa que el evento aleatorio es imposible y, como tal, nunca tendrá lugar. Hacia la mitad de la línea de probabilidad, las posibilidades de que ocurra el evento son iguales o ½. A la derecha, tenemos 1, lo que significa que es muy probable que ocurra el evento aleatorio.

En la ruleta, la probabilidad de ganar con tipos de apuesta específicos es bastante fácil de determinar. Como sabemos, hay 37 o 38 resultados posibles por giro simple, dependiendo de si uno está jugando en una rueda de cero simple o doble cero. Dado que los resultados en los juegos de ruleta son completamente aleatorios, solo hay dos resultados posibles para los jugadores: ganan o pierden.

Por lo tanto, la probabilidad de ganar con un tipo de apuesta determinado se calcula dividiendo el número de formas de ganar por el número total de todos los resultados posibles. Otra forma de decirlo sería decir que la probabilidad de ganar es igual al número de formas de ganar, dividido por el total de formas de ganar y las formas de perder.

A partir de esto, se deduce que podemos calcular la probabilidad de ganar con una determinada apuesta de ruleta utilizando la siguiente fórmula: Probabilidad de ganar = Formas de ganar / (Formas de ganar + Formas de perder). Primero demostremos cómo funciona usando el lanzamiento de una moneda como ejemplo.

Como sabes, cuando lanzas una moneda, solo hay dos resultados posibles, ya que la moneda caerá en cara o cruz. Las posibilidades de que caiga en cada uno de los dos lados son prácticamente iguales. Usando la fórmula anterior, realizaríamos el siguiente cálculo: Probabilidad de caras = 1/1 + 1 = 0.50. Para convertir este resultado en un porcentaje, multiplicamos por 100 y obtenemos 50%.

Ahora, apliquemos la fórmula anterior para calcular la probabilidad de cobrar un pago con una apuesta dividida en el juego de la ruleta. Dado que con las apuestas divididas los jugadores cubren solo dos números adyacentes en el diseño, solo hay dos formas de ganar de 37 posibles resultados, es decir, si uno está jugando en una ruleta europea de un solo cero. Otra forma de decirlo sería decir que hay dos formas de ganar y 35 formas de perder con su apuesta dividida. Por lo tanto, el cálculo será el siguiente: 2 / (2 + 35) = 0.0540 x 100 = 5.40%. Por el contrario, la probabilidad de ganar con la misma apuesta en la ruleta americana se reduce al 5,26%, lo que coincide con la ventaja de la casa en los juegos de doble cero.

Cuanto mayor sea el número de resultados que cubra con una sola apuesta, mayor será la probabilidad de ganar. Por ejemplo, supongamos que está interesado en experimentar con una de las apuestas de ruleta más exóticas, como Voisin du Zero, que cubre una secuencia de diecisiete números aleatorios en la rueda de un solo cero. La probabilidad de acertar uno de estos números ganadores es igual al 45,94% o 17 / (17 + 20) x 100, ya que ahora está cubriendo casi la mitad de toda la rueda con una de esas apuestas. Como probablemente pueda ver por sí mismo, calcular la probabilidad de ganar con diferentes tipos de apuestas de ruleta no requiere un conocimiento matemático profundo.

Las probabilidades de las apuestas en la ruleta

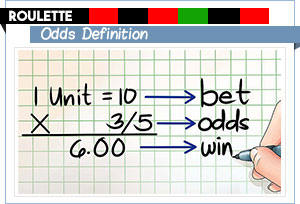Las reglas que se aplican en las mesas de casino están diseñadas de tal manera que inclinan la ventaja a favor de la casa.Debido a esto, es de extrema importancia que los jugadores de ruleta aprendan a calcular las probabilidades de ganar con cada tipo de apuesta.

Algunas personas creen falsamente que los términos «probabilidades» y «probabilidad» se pueden usar indistintamente cuando en realidad no pueden, simplemente porque denotan dos nociones diferentes. Si no está familiarizado con el término «probabilidades», indica la relación entre el número de formas de ganar y el número de formas de perder. A diferencia de la probabilidad, las probabilidades nunca se expresan en términos de porcentajes, sino que normalmente se presentan como pares de números.

Las probabilidades de un evento aleatorio, como el lanzamiento de un dado o un giro en la ruleta, indican la probabilidad de que se produzca este evento. Para calcular las probabilidades de ganar con una determinada apuesta de ruleta, debe averiguar qué su probabilidad es. Entonces puede usar la siguiente fórmula: Probabilidades de ganar = Probabilidad de ganar / (1 – Probabilidad de ganar). Si usamos el ejemplo de lanzamiento de moneda anterior, el cálculo será el siguiente: 0.5 / (1 – 0.5) = 1/1 que también se puede expresar como 1 a 1. Las probabilidades en este caso son pares.

Sin embargo, hay una manera más fácil de calcular las probabilidades de ganar con las apuestas de ruleta y es simplemente dividir el número de formas de ganar por el número de formas de perder. Por lo tanto, las probabilidades de ganar con un Straight Up son t en 32 rojo, por ejemplo, se expresaría como probabilidades de ganar = 1/36 o 1 a 36, porque solo hay un número ganador y 36 números que resultan en una pérdida. Como puede ver, la probabilidad difiere de las probabilidades en que es una probabilidad de 1 de 37 resultados. De manera similar, las probabilidades de ganar con la apuesta dividida del ejemplo anterior serían de 2 a 35 o 2/35.

Algunos jugadores de ruleta tienden a confundir las probabilidades de ganar con las probabilidades de ganar porque la proporción está escrita al revés en muchas ocasiones, como 36 a 1. Esto no es exactamente lo mismo porque las probabilidades en contra un evento dado refleja la probabilidad de que dicho evento no suceda. En este caso, la fórmula para calcular las probabilidades en contra de una determinada apuesta ganadora también se invertirá así: Probabilidades en contra de ganar = Maneras de perder / Maneras de ganar. Por lo tanto, las probabilidades de ganar con una apuesta directa al 32 rojo son iguales a 36/1.

Los establecimientos de juego suelen utilizar estas probabilidades invertidas para enumerar los pagos de las apuestas ganadoras. Cuanto menor sea la probabilidad de ganar con una determinada apuesta de ruleta, mayor será el rendimiento ofrecido por la casa. Esto es así porque cuando se trata de la mayoría de los juegos de casino, incluida la ruleta, los jugadores prácticamente compiten contra la casa. Por lo tanto, la casa está apostando contra sus patrocinadores, por lo que las probabilidades pagadas son las probabilidades en contra de que el jugador gane, de ahí la razón invertida. Podrá leer información más detallada sobre las probabilidades de la casa en la sección siguiente.

Las probabilidades del casino y cómo se reflejan en la rentabilidad de los jugadores

En lo que respecta a los juegos de casino, siempre existe una disparidad entre la probabilidad matemática de ganar con sus apuestas y la proporción en la que se pagan estas apuestas. Es precisamente esta disparidad entre las probabilidades reales de ganar y las probabilidades del casino lo que le da a la casa una ventaja sobre los jugadores a largo plazo.

Para cada juego que ofrece el casino, las probabilidades de pago de las apuestas se establecen de tal manera que el casino puede generar ganancias en cada apuesta que realice. Esta ventaja de la casa se expresa en porcentajes que reflejan el rendimiento general que el casino puede esperar con el tiempo, o en otras palabras, el porcentaje promedio que los jugadores inevitablemente perderán a largo plazo. Al ser un negocio comercial, el casino necesita su ventaja para cubrir los costos asociados con el hospedaje de los juegos. La conclusión es que no importa cuán pequeña sea esta ventaja, aún puede mermar el bankroll con el tiempo.

En algunos juegos de azar como los dados, hay grandes fluctuaciones en la ventaja de la casa para diferentes tipos de apuestas. . Este no es el caso en la ruleta donde la ventaja permanece constante, con una sola excepción que es la apuesta de cinco números. Este último solo se puede hacer en juegos de doble cero y le da a la casa una ventaja del 7.89%.

Para calcular la ventaja de la casa en la ruleta, multiplicamos la diferencia entre las probabilidades reales en contra de ganar y las probabilidades del casino por la probabilidad de ganar. En una rueda de doble cero, las probabilidades de ganar con una apuesta directa son 37 a 1, pero la casa paga solo 35 a 1, lo que da como resultado una ventaja de la casa del 5,26%. Como puede ver, la diferencia entre las probabilidades de ganar y el pago en la ruleta americana es igual a dos unidades. Usando la fórmula anterior, podemos calcular la ventaja de la casa así:

(37/1 – 35/1) x 1/38 = 2/1 x 1/38 = 0.0526 x 100 = 5.26%

La ventaja de la casa en la ruleta europea es significativamente menor porque solo hay una casilla de cero en la rueda, por lo que el cálculo se ejecutará de la siguiente manera:

(36/1 – 35/1) x 1/37 = 1/1 x 1/37 = 0.0270 x 100 = 2.70%.

En otras palabras, los jugadores enfrentarán pérdidas de 27 £ en promedio por cada 1000 £ que apuesten en la ruleta europea. Tenga en cuenta que puede esperar tales pérdidas solo durante períodos prolongados de tiempo que implican decenas de miles de giros. Todo es posible a corto plazo, por lo que los jugadores ciertamente pueden estar por delante si apuestan a la ruleta de forma recreativa durante uno o dos días.

De manera similar, las probabilidades de ganar con una apuesta de esquina (que cubre cuatro números adyacentes en el diseño) son 33 a 4 en una rueda de un solo cero, pero el casino paga a los jugadores solo 32 a 4, lo que significa que la casa obtiene una ganancia de una unidad de todas las apuestas de esquina ganadoras. En la ruleta americana, donde hay dos ceros en la rueda, el casino se beneficiará con dos unidades en tales apuestas porque las probabilidades en contra de ganar aumentan aún más de 34 a 4, pero las probabilidades de pago siguen siendo de 32 a 4.

En juegos de azar como la ruleta, no hay forma de escapar de la ventaja de la casa: cuanto más juegues, más perderás a largo plazo. Por eso, la variación de la ruleta que uno juega es de gran consecuencia para su rentabilidad general a largo plazo. Tiene sentido que jugar con ruedas de un solo cero sea más rentable para los jugadores, especialmente si las Reglas de La Partage o En Prison están vigentes, ya que disminuyen la ventaja del casino al 1.36%.

Cálculo de las probabilidades de números consecutivos

Algunos jugadores cometen el error de agrupar dos o más resultados sucesivos de la ruleta creyendo que la ganancia anterior los números impactan los resultados en los siguientes giros. Estos jugadores pueden presenciar la llegada del negro cuatro veces seguidas y asumir incorrectamente que la probabilidad de que el rojo aparezca a continuación es mayor porque la bola no ha aterrizado en una tronera roja durante un tiempo.

La verdad del asunto es que esta línea de pensamiento es incorrecta porque la probabilidad de ganar con cualquier número individual es siempre la misma, sin importar cuántas veces seguidas haya ganado este número. Sin embargo, es posible calcular la probabilidad combinada de ganar con una determinada apuesta de ruleta dos, tres o más veces seguidas. Usemos la apuesta directa al 9 rojo en la ruleta europea como ejemplo para demostrar cómo se hace.

La probabilidad combinada de ganar con 9 rojo dos veces consecutivas es el resultado de la multiplicación de las probabilidades individuales de que este número salga o sea 1/37 x 1/37 = 1/1369. La probabilidad de ganar con 9 rojas disminuye con cada repetición posterior. Por lo tanto, la probabilidad de que este número individual aparezca tres veces seguidas es igual a 1/37 x 1/37 x 1/37 = 1/50653.

La probabilidad de ganar con 9 rojas en cualquier el giro es siempre el mismo o 1/37. Pero ganar con el mismo número individual tres, cuatro o más veces seguidas es evidentemente una ocurrencia rara. Como puede ver en el cálculo anterior, acertar el mismo número tres veces consecutivas equivale a 1 probabilidad entre 50,653. Esto corresponde a una probabilidad del 0,0019% de ganar con el mismo número tres veces seguidas.
Tenga en cuenta que repetir los resultados de la ruleta por sí mismos no es un fenómeno tan raro. Es probable que un número se repita en promedio una vez por cada 37 lanzamientos de la pelota, es decir, es probable que el 9 rojo golpee aproximadamente dos veces por hora. Es la repetición consecutiva del número lo que es un evento raro.

Cálculo de las probabilidades de las rachas

Las rachas suelen ocurrir con apuestas de dinero par en las que las posibilidades de ganar y perder son casi iguales. Siguiendo la misma línea de razonamiento de la sección anterior, establecemos que la probabilidad de ganar con una apuesta de dinero par a las negras es igual a 18/37 en una rueda europea, ya que hay 18 casillas ganadoras de 37.

Si el rojo ha golpeado tres veces consecutivas, la probabilidad de que aparezca el próximo negro sigue siendo 18/37. Lo mismo es válido para los golpes rojos en el cuarto giro. De hecho, esto se aplica a todas las apuestas de dinero par, ya sea alta / baja, roja / negra o impar / par, ya que la probabilidad de cada uno de estos resultados es siempre 18/37 en una rueda de un solo cero. Poco importa cuál fue el resultado del giro anterior.

La probabilidad de que ocurra una racha ganadora con apuestas de dinero par se calcula de la misma manera que la de que los números individuales ganen varias veces seguidas. En otras palabras, necesitamos multiplicar las probabilidades individuales del resultado. Así, la probabilidad de tener una buena racha con negras ganando tres veces consecutivas sería igual a 18/37 x 18/37 x 18/37 = 5832/50653 = 1 / 8,68. Por lo tanto, es probable que esa racha ocurra una vez cada ocho lanzamientos y medio de la pelota en promedio.

También es posible averiguar cuál es la probabilidad de una racha perdedora. Dado que las apuestas de dinero par pierden cada vez que la bola cae en la casilla cero verde, la probabilidad de perder con las negras, por ejemplo, es de 19/37 en una rueda europea porque hay 19 formas de perder de 37 posibles resultados.La fórmula para una racha perdedora es la misma que para una racha ganadora. La probabilidad de perder tres veces seguidas con negras es 19/37 x 19/37 x 19/37 = 6859/50653 = 1 / 7.38. Es decir, experimentará tres pérdidas consecutivas con apuestas de dinero par una vez por cada 7,4 en promedio.

• Ruleta americana
• Los mejores sitios de ruleta con dinero real
• Los mejores sistemas de ruleta
• Double Action Roulette
• Double Ball Roulette
• Ruleta europea
• Ruleta francesa
• Ruleta High Roller
• La ruleta más popular Juegos
• Juegue a la ruleta en línea
• Ruleta con bote progresivo
• Apuestas de ruleta y patrones de apuestas
• Reglas de la ruleta
• Ruleta Estrategias
• Variaciones de la ruleta