Hurtig sorteringsalgoritme

Hurtig sortering er en af de forskellige sorteringsteknikker, der er baseret på konceptet Divide and Conquer, ligesom flet sort. Men i hurtig sortering udføres alt det tunge løft (større arbejde), mens man opdeler arrayet i underarrays, mens i tilfælde af flettsortering sker alt det virkelige arbejde under fletning af subarrays. I tilfælde af hurtig sortering gør kombineringstrinnet intet.

Det kaldes også partition-exchange sort. Denne algoritme opdeler listen i tre hoveddele:

1. Elementer mindre end Pivot-elementet
2. Pivot-element (Central element)
3. Elementer større end pivotelement

Pivotelement kan være ethvert element fra arrayet, det kan være det første element, det sidste element eller et vilkårligt element. I denne tutorial tager vi elementet til højre eller det sidste element som drejning.

For eksempel: I array {52, 37, 63, 14, 17, 8, 6, 25} tager vi 25 som omdrejningspunkt. Så efter det første pass ændres listen sådan.

{6 8 17 14 25 63 37 52}

Derefter efter den første pasning vil drejning blive indstillet til sin position, hvor alle elementerne er mindre til venstre for den og alle elementerne større end til højre. Nu betragtes 6 8 17 14 og 63 37 52 som to separate solarrays, og samme rekursive logik vil blive anvendt på dem, og vi fortsætter med at gøre dette indtil hele arrayet er sorteret.

Hvordan fungerer hurtig sortering?

Følgende er de trin, der er involveret i hurtig sorteringsalgoritme:

1. Efter at have valgt et element som pivot, som er det sidste indeks for arrayet i vores tilfælde, deler vi arrayet for første gang.
2. I hurtig sortering kalder vi denne partitionering. Det er ikke simpelt at nedbryde array i 2 subarrays, men i tilfælde af partitionering er arrayelementerne så placeret, at alle de elementer, der er mindre end pivot, vil være på venstre side af pivot, og alle elementerne større end pivot vil være på højre side af det.
3. Og drejningselementet vil være i sin endelige sorterede position.
4. Elementerne til venstre og højre sorteres muligvis ikke.
5. Derefter vælger vi underarrays, elementer til venstre for pivot og elementer til højre for pivot, og vi udfører partitionering på dem ved at vælge en pivot i subarrays.

Lad os se på en matrix med værdier {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Nedenfor har vi en billedlig gengivelse af, hvor hurtig sortering vil sortere det givne array.

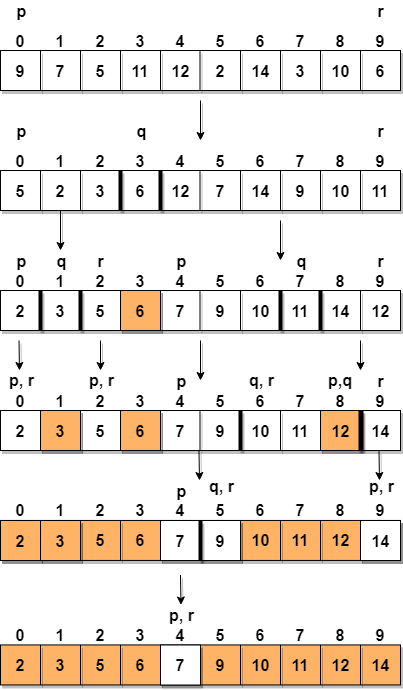
I trin 1 vælger vi det sidste element som pivot, hvilket er 6 i dette tilfælde, og kalder på partitioning, og derfor omarrangere g arrayet på en sådan måde, at 6 placeres i sin endelige position og til venstre vil alle elementerne være mindre end det og til højre, vil vi have alle elementerne større end det.

Derefter vælger vi underarray til venstre og subarray til højre og vælger en drejetap til dem. I ovenstående diagram valgte vi 3 som pivot for det venstre subarray og 11 som pivot for det højre subarray.

Og vi opfordrer igen til partitioning.

Implementering af hurtig sorteringsalgoritme

Nedenfor har vi et simpelt C-program, der implementerer hurtig sorteringsalgoritmen:

Kompleksitetsanalyse af hurtig sortering

For en matrix, hvor partitionering fører til ubalancerede underarrays, i et omfang hvor der på venstre side ikke er nogen elementer med alle elementerne større end omdrejningspunktet, dermed på højre side.

Og hvis du fortsætter med at få ubalancerede underarrays, så løber ning tid er det værste tilfælde, som er O(n2)

Hvor som om partitionering fører til næsten lige store subarrays, så er køretiden den bedste med tidskompleksitet som O (n * log n).

Kompleksitet i værste tilfælde tid: O (n2)

Kompleksitet i bedste tilfælde tid: O (n * log n)

Gennemsnitlig tidskompleksitet: O (n * log n)

Rumkompleksitet: O (n * log n)

Som vi ved nu, at hvis subarrays partitionering produceres efter partitionering er ubalanceret, vil hurtig sortering tage mere tid at afslutte. Hvis nogen ved, at du vælger det sidste indeks som pivot hele tiden, kan de med vilje give dig matrix, hvilket vil resultere i worst-case driftstid for hurtig sortering.

For at undgå dette kan du vælge tilfældigt drejelement også. Det vil ikke gøre nogen forskel i algoritmen, da alt hvad du skal gøre er at vælge et tilfældigt element fra arrayet, bytte det med element i det sidste indeks, gøre det til omdrejningspunktet og fortsætte med hurtig sortering.

• Plads krævet af hurtig sortering er meget mindre, kun O(n*log n) yderligere plads kræves.
• Hurtig sortering er ikke en stabil sorteringsteknik, så det kan ændre forekomsten af to lignende elementer på listen under sortering.

Nu hvor vi har lært Hurtig sortering algoritme, kan du også tjekke disse sorteringsalgoritmer og deres applikationer:

• Indsætningssortering
• Valgsortering
• Boblesortering
• Flet sort
• Heap Sort
• Counting Sort