Quick Sort Algorithm (Norsk)

Quick Sort er en av de forskjellige sorteringsteknikkene som er basert på konseptet Divide and Conquer, akkurat som slå sammen. Men i rask sortering blir alt tungt løfting (større arbeid) gjort mens du deler opp matrisen i underarrays, mens i tilfelle sammenslåing av sortering skjer alt det virkelige arbeidet under sammenslåing av underarrangementene. Ved rask sortering, gjør kombinertrinnet absolutt ingenting.

Det kalles også partisjon-utvekslingssorter. Denne algoritmen deler listen i tre hoveddeler:

1. Elementer mindre enn Pivot-elementet
2. Pivot-element (Central element)
3. Elementer større enn pivotelement

Pivotelement kan være hvilket som helst element fra matrisen, det kan være det første elementet, det siste elementet eller et vilkårlig element. I denne opplæringen tar vi elementet til høyre eller det siste elementet som pivot.

For eksempel: I matrisen {52, 37, 63, 14, 17, 8, 6, 25} tar vi 25 som pivot. Så etter første passering vil listen endres slik.

{6 8 17 14 25 63 37 52}

Derfor blir pivot etter første passering satt i sin posisjon, med alle elementene mindre til venstre og alle elementene større enn til høyre. Nå blir 6 8 17 14 og 63 37 52 betraktet som to separate solstråler, og samme rekursive logikk vil bli brukt på dem, og vi vil fortsette å gjøre dette til hele matrisen er sortert.

Hvordan fungerer rask sortering?

Følgende er trinnene involvert i hurtig sorteringsalgoritme:

1. Etter at du har valgt et element som pivot, som er den siste indeksen til matrisen i vårt tilfelle, deler vi matrisen for første gang.
2. I rask sortering kaller vi denne partisjonering. Det er ikke enkelt å dele opp matrisen i to underarrays, men i tilfelle partisjonering er matriseelementene så plassert at alle elementene som er mindre enn pivoten, vil være på venstre side av pivoten, og alle elementene større enn pivot vil være på høyre side av det.
3. Og pivotelementet vil være i sin endelige sorterte posisjon.
4. Elementene til venstre og høyre kan ikke sorteres.
5. Deretter velger vi underarrays, elementer til venstre for pivot og elementer til høyre for pivot, og vi utfører partisjonering på dem ved å velge en pivot i subarrays.

La oss se på en matrise med verdier {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Nedenfor har vi en illustrasjon av hvor rask sortering vil sortere den gitte matrisen.

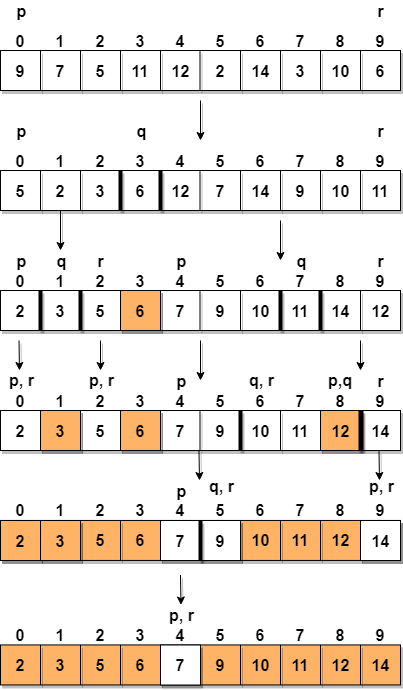
I trinn 1 velger vi det siste elementet som pivot, som er 6 i dette tilfellet, og ring partitioning, og omorganiser g matrisen på en slik måte at 6 vil bli plassert i sin endelige posisjon og til venstre vil alle elementene være mindre enn den og til høyre, vil vi ha alle elementene større enn det.

Så plukker vi undergruppen til venstre og undergruppen til høyre og velger en pivot for dem. I diagrammet ovenfor valgte vi 3 som pivot for venstre subarray og 11 som pivot for høyre subarray.

Og vi kaller igjen partitioning.

Implementering av hurtig sorteringsalgoritme

Nedenfor har vi et enkelt C-program som implementerer hurtig sorteringsalgoritmen:

Kompleksitetsanalyse av rask sortering

For en matrise der partisjonering fører til ubalanserte underarrayer, i en grad der det ikke er noen elementer på venstre side, med alle elementene større enn pivoten, derav på høyre side.

Og hvis du fortsetter å få ubalanserte underarrays, så løp ningstid er det verste tilfellet, som er O(n2)

Hvor som om partisjonering fører til nesten like underarrangementer, er kjøretiden den beste, med tidskompleksitet som O (n * log n).

Kompleksitet i verste tilfelle: O (n2)

Kompleksitet i beste tilfelle: O (n * log n)

Gjennomsnittlig tidskompleksitet: O (n * log n)

Romkompleksitet: O (n * log n)

Som vi vet nå, at hvis subarrays partisjonering produsert etter partisjonering er ubalansert, vil rask sortering ta mer tid å fullføre. Hvis noen vet at du velger den siste indeksen som pivot hele tiden, kan de med vilje gi deg en matrise som vil resultere i verst mulig kjøretid for rask sortering.

For å unngå dette, kan du velge tilfeldig dreieelement også. Det vil ikke utgjøre noen forskjell i algoritmen, ettersom alt du trenger å gjøre er å velge et tilfeldig element fra matrisen, bytte det ut med elementet ved den siste indeksen, gjøre det til omdreining og fortsette med rask sortering.

• Plass som kreves av rask sortering er veldig mindre, bare O(n*log n) ekstra plass kreves.
• Rask sortering er ikke en stabil sorteringsteknikk, så det kan endre forekomsten av to like elementer i listen mens du sorterer.

Nå som vi har lært Rask sortering algoritme, kan du også sjekke ut disse sorteringsalgoritmene og deres applikasjoner:

• Innsettingssortering
• Valgsortering
• Bubblesortering
• Merge sort
• Heap Sort
• Counting Sort