Algorithme de tri rapide

Le tri rapide est lune des différentes techniques de tri qui est basée sur le concept de Divide and Conquer, tout comme tri par fusion. Mais dans le tri rapide, tout le gros du travail (travail majeur) est effectué en divisant le tableau en sous-tableaux, tandis quen cas de tri par fusion, tout le vrai travail se produit lors de la fusion des sous-tableaux. En cas de tri rapide, létape de combinaison ne fait absolument rien.

Elle est aussi appelée tri déchange de partition. Cet algorithme divise la liste en trois parties principales:

1. Éléments inférieurs à lélément Pivot
2. Élément Pivot (élément central)
3. Éléments supérieurs à lélément élément pivot

Lélément pivot peut être nimporte quel élément du tableau, il peut être le premier élément, le dernier élément ou tout élément aléatoire. Dans ce tutoriel, nous prendrons lélément le plus à droite ou le dernier élément comme pivot.

Par exemple: Dans le tableau {52, 37, 63, 14, 17, 8, 6, 25}, nous prenons 25 comme pivot. Ainsi, après le premier passage, la liste sera modifiée comme ceci.

{6 8 17 14 25 63 37 52}

Donc après le premier passage, le pivot sera mis à sa position, avec tous les éléments plus petits à sa gauche et tous les éléments plus grands quà sa droite. Désormais, 6 8 17 14 et 63 37 52 sont considérés comme deux matrices solaires distinctes, et la même logique récursive leur sera appliquée, et nous continuerons à faire le tableau complet est trié.

Comment fonctionne le tri rapide?

Voici les étapes impliquées dans lalgorithme de tri rapide:

1. Après avoir sélectionné un élément comme pivot, qui est le dernier index du tableau dans notre cas, nous divisons le tableau pour la première fois.
2. En tri rapide, nous appelons ce partitionnement. Ce nest pas une simple décomposition du tableau en 2 sous-tableaux, mais en cas de partitionnement, les éléments du tableau sont positionnés de telle sorte que tous les éléments plus petits que le pivot seront sur le côté gauche du pivot et tous les éléments plus grands que le pivot seront être sur le côté droit de celui-ci.
3. Et lélément pivot sera à sa position finale triée.
4. Les éléments à gauche et à droite ne peuvent pas être triés.
5. Ensuite, nous choisissons des sous-tableaux, des éléments à gauche du pivot et des éléments à droite du pivot, et nous effectuons un partitionnement sur eux en choisissant un pivot dans les sous-tableaux.

Considérons un tableau avec des valeurs {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Ci-dessous, nous avons une représentation graphique de la rapidité avec laquelle le tri triera le tableau donné.

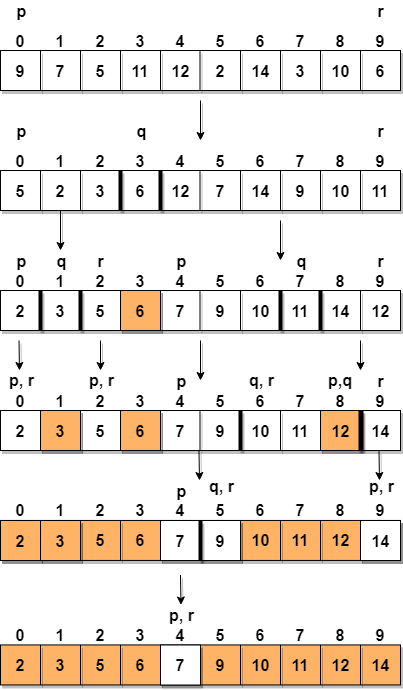
À létape 1, nous sélectionnons le dernier élément comme pivot, qui est 6 dans ce cas, et appelez partitioning, donc réorganisez g le tableau de telle manière que 6 sera placé dans sa position finale et à sa gauche se trouveront tous les éléments inférieurs à lui et à sa droite, nous aurons tous les éléments plus grand que cela.

Ensuite, nous choisissons le sous-tableau à gauche et le sous-tableau à droite et sélectionnons un pivot pour eux, dans le diagramme ci-dessus, nous avons choisi 3 comme pivot pour le sous-tableau de gauche et 11 comme pivot pour le sous-tableau de droite.

Et nous appelons à nouveau partitioning.

Implémentation de lalgorithme de tri rapide

Ci-dessous, nous avons un programme C simple implémentant lalgorithme de tri rapide:

Analyse de complexité du tri rapide

Pour un tableau, dans lequel le partitionnement conduit à des sous-tableaux déséquilibrés, à un point où sur le côté gauche il ny a pas déléments, avec tous les éléments plus grand que le pivot, donc sur le côté droit.

Et si vous continuez à avoir des sous-tableaux déséquilibrés, alors la course ning time est le pire des cas, qui est O(n2)

Où, comme si le partitionnement conduisait à des sous-tableaux presque égaux, alors le temps dexécution est le meilleur, avec une complexité temporelle comme O (n * log n).

Complexité temporelle du pire cas: O (n2)

Complexité temporelle du meilleur cas: O (n * log n)

Complexité temporelle moyenne: O (n * log n)

Complexité spatiale: O (n * log n)

Comme nous le savons maintenant, si le partitionnement des sous-tableaux se produit après le partitionnement sont déséquilibrés, le tri rapide prendra plus de temps. Si quelquun sait que vous choisissez le dernier index comme pivot tout le temps, il peut intentionnellement vous fournir un tableau qui entraînera le pire des cas dexécution pour un tri rapide.

Pour éviter cela, vous pouvez choisir au hasard élément pivot aussi. Cela ne fera aucune différence dans lalgorithme, car tout ce que vous avez à faire est de choisir un élément aléatoire dans le tableau, de léchanger avec lélément au dernier index, den faire le pivot et de continuer avec un tri rapide.

• Lespace requis par le tri rapide est très inférieur, seul O(n*log n) lespace supplémentaire est requis.
• Le tri rapide nest pas une technique de tri stable, il peut donc changer lapparition de deux éléments similaires dans la liste lors du tri.

Maintenant que nous avons appris le tri rapide algorithme de tri, vous pouvez également consulter ces algorithmes de tri et leurs applications:

• Tri par insertion
• Tri par sélection
• Tri par bulles
• Tri par fusion
• Tri par tas
• Tri par comptage