Pikalajittelualgoritmi

Pikalajittelu on yksi erilaisista lajittelutekniikoista, joka perustuu jakamisen ja valloittamisen käsitteeseen aivan kuten Yhdistä lajittelu. Mutta pikalajittelussa kaikki raskaat nostot (suuret työt) tehdään jakamalla matriisi alirakenteisiin, kun taas yhdistämislajittelun tapauksessa kaikki todelliset työt tapahtuvat alirakenteiden yhdistämisen aikana. Jos kyseessä on nopea lajittelu, yhdistämisvaihe ei tee mitään.

Sitä kutsutaan myös osionvaihtolajitteluksi. Tämä algoritmi jakaa luettelon kolmeen pääosaan:

1. Pivot-elementtiä pienemmät elementit
2. Pivot-elementti (Central-elementti)
3. Elementit, jotka ovat suurempia kuin pivot-elementti

Pivot-elementti voi olla mikä tahansa matriisin elementti, se voi olla ensimmäinen elementti, viimeinen elementti tai mikä tahansa satunnainen elementti. Tässä opetusohjelmassa otamme oikeanpuoleisen elementin tai viimeisen elementin pivotiksi.

Esimerkiksi: Otetaan taulukossa {52, 37, 63, 14, 17, 8, 6, 25} 25 pivotina. Joten ensimmäisen kierroksen jälkeen luetteloa muutetaan näin.

{6 8 17 14 25 63 37 52}

Ensimmäisen kierroksen jälkeen kääntö asetetaan siten, että kaikki elementit ovat sitä pienempiä vasemmalla ja kaikki suuremmat kuin oikealla. Nyt 6 8 17 14 ja 63 37 52 pidetään kahtena erillisenä aurinkosäteenä, ja niihin sovelletaan samaa rekursiivista logiikkaa, ja jatkamme tätä, kunnes koko taulukko on lajiteltu.

Kuinka pikalajittelu toimii?

Seuraavassa on pikalajittelualgoritmin vaiheet:

1. Kun olet valinnut elementin pivot, joka on tapauksemme matriisin viimeinen hakemisto, jaamme matriisin ensimmäistä kertaa.
2. Pikalajittelussa kutsumme tätä osioksi. Matriisin jakaminen kahteen aliryhmään ei ole yksinkertaista, mutta osioinnin tapauksessa taulukkoelementit on sijoitettu niin, että kaikki saranaa pienemmät elementit ovat kääntymän vasemmalla puolella ja kaikki saranaa suuremmat elementit olla sen oikealla puolella.
3. Ja kääntöelementti on lopullisessa lajittelupaikassaan.
4. Vasemmalle ja oikealle olevia elementtejä ei voida lajitella.
5. Sitten valitsemme alisäteet, elementit saranan vasemmalle puolelle ja elementit saranan oikealle puolelle, ja suoritamme osioinnin niille valitsemalla saranan aliriville.

Tarkastellaan matriisia, jonka arvot ovat {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Alla on kuvallinen kuvaus siitä, kuinka nopea lajittelu lajittelee annetun taulukon.

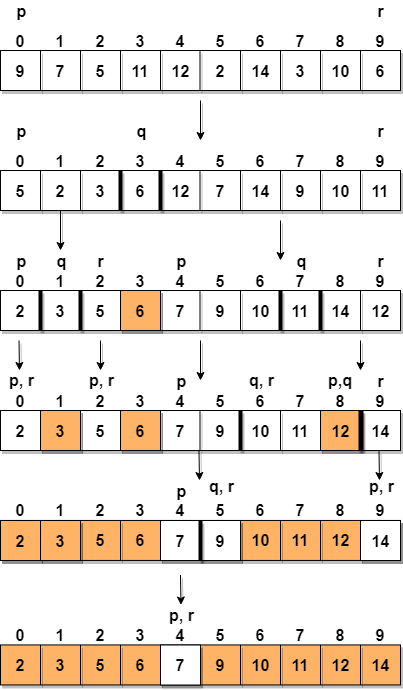
Vaiheessa 1 valitaan viimeinen elementti pivot, joka on 6 tässä tapauksessa, ja soita partitioning, joten järjestä uudelleen g taulukko siten, että 6 sijoitetaan lopulliseen sijaintiinsa ja vasemmalla puolella on kaikki sen alapuolella olevat elementit ja oikealla puolella, meillä on kaikki elementit suurempi kuin se.

Sitten valitsemme alapiirin vasemmalta ja alaosan oikealta ja valitsemme heille pivotin. Yllä olevasta kaaviosta valitsimme 3 pivotina vasempaan alikentään ja 11 pivotina oikeaan alaosaan.

Ja pyydämme jälleen partitioning.

Pikalajittelualgoritmin toteuttaminen

Alla on yksinkertainen C-ohjelma, joka toteuttaa pikalajittelualgoritmin:

Pikalajittelun monimutkaisuusanalyysi

Matriisille, jossa osiointi johtaa epätasapainoisiin alirakenteisiin siinä määrin, että vasemmalla puolella ei ole elementtejä, kaikki elementit suurempi kuin kääntö, siis oikealla puolella.

Ja jos jatkat epätasapainoista osariviä, niin juoksu Ja-aika on pahin tapaus, joka on O(n2)

Missä ikään kuin osiointi johtaa melkein yhtä suuriin aliriveihin, niin juoksuaika on paras, aika monimutkaisempi kuin O (n * log n).

Pahimman tapauksen ajan monimutkaisuus: O (n2)

Parhaan tapauksen ajan monimutkaisuus: O (n * log n)

Keskimääräinen ajan monimutkaisuus: O (n * log n)

Avaruuden monimutkaisuus: O (n * log n)

Kuten tiedämme nyt, että jos aliyhdistelmät muodostavat osituksen osituksen jälkeen ovat epätasapainossa, nopea lajittelu vie enemmän aikaa loppuun. Jos joku tietää, että valitset viimeisen hakemiston pivotina koko ajan, hän voi tarkoituksellisesti antaa sinulle taulukon, joka johtaa pahimpaan mahdolliseen ajoaikaan nopeaa lajittelua varten.

Tämän välttämiseksi voit valita satunnaisen myös kääntöelementti. Se ei tee mitään eroa algoritmissa, koska sinun tarvitsee vain valita satunnaiselementti taulukosta, vaihtaa se viimeisen hakemiston elementillä, tehdä siitä kääntö ja jatkaa pikalajittelua.

• Pikalajittelun vaatima tila on hyvin pieni, vain O(n*log n) lisätilaa tarvitaan.
• Pikalajittelu ei ole vakaa lajittelutekniikka, joten se voi muuttaa luettelossa kahden samanlaisen elementin esiintymistä lajittelun aikana.

Nyt kun olemme oppineet pikalajittelun algoritmi, voit tarkistaa myös nämä lajittelualgoritmit ja niiden sovellukset:

• lisäyslajittelu
• valintalajittelu
• kuplalajittelu
• Yhdistä lajittelu
• Kasan lajittelu
• Lajittelulaji