Algoritmo de clasificación rápida

La clasificación rápida es una de las diferentes técnicas de clasificación que se basa en el concepto de dividir y conquistar, al igual que fusionar ordenación. Pero en la ordenación rápida, todo el trabajo pesado (trabajo principal) se realiza mientras se divide la matriz en subarreglos, mientras que en el caso de la ordenación por fusión, todo el trabajo real ocurre durante la fusión de los subarreglos. En caso de clasificación rápida, el paso de combinación no hace absolutamente nada.

También se denomina clasificación de intercambio de partición. Este algoritmo divide la lista en tres partes principales:

1. Elementos menores que el elemento Pivot
2. Elemento Pivot (elemento central)
3. Elementos mayores que el elemento pivote

El elemento pivote puede ser cualquier elemento de la matriz, puede ser el primer elemento, el último elemento o cualquier elemento aleatorio. En este tutorial, tomaremos el elemento más a la derecha o el último elemento como pivote.

Por ejemplo: En la matriz {52, 37, 63, 14, 17, 8, 6, 25}, tomamos 25 como pivote. Entonces, después de la primera pasada, la lista cambiará así.

{6 8 17 14 25 63 37 52}

Por lo tanto, después de la primera pasada, pivot se establecerá en su posición, con todos los elementos más pequeños a su izquierda y todos los elementos más grandes que a su derecha. Ahora 6 8 17 14 y 63 37 52 se consideran dos matrices solares separadas, y se les aplicará la misma lógica recursiva, y seguiremos haciendo esto hasta la matriz completa está ordenada.

¿Cómo funciona la ordenación rápida?

Los siguientes son los pasos involucrados en el algoritmo de ordenación rápida:

1. Después de seleccionar un elemento como pivot, que es el último índice de la matriz en nuestro caso, dividimos la matriz por primera vez.
2. En clasificación rápida, lo llamamos partición. No es simple dividir el arreglo en 2 subarreglos, pero en el caso de la partición, los elementos del arreglo están colocados de manera que todos los elementos más pequeños que el pivote estarán en el lado izquierdo del pivote y todos los elementos mayores que el pivote estarán estar en el lado derecho.
3. Y el elemento pivote estará en su posición final ordenada.
4. Los elementos a la izquierda y a la derecha, pueden no estar ordenados.
5. Luego seleccionamos subarreglos, elementos a la izquierda del pivote y elementos a la derecha del pivote, y realizamos particiones en ellos eligiendo un pivote en los subarreglos.

Consideremos una matriz con valores {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

A continuación, tenemos una representación gráfica de qué tan rápido clasificará la matriz dada.

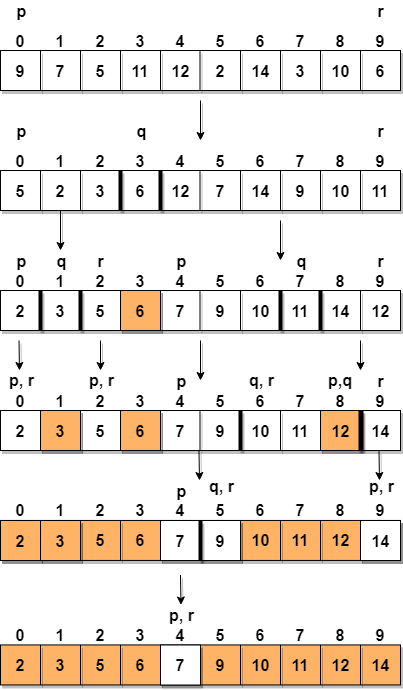
En el paso 1, seleccionamos el último elemento como el pivot, que es 6 en este caso, y llama a partitioning, por lo tanto, reorganiza g el arreglo de tal manera que 6 se colocará en su posición final y a su izquierda estarán todos los elementos menores que él ya su derecha, tendremos todos los elementos mayor que él.

Luego elegimos el subarreglo de la izquierda y el subarreglo de la derecha y seleccionamos un pivote para ellos, en el diagrama de arriba, elegimos 3 como pivote para el subarreglo izquierdo y 11 como pivote para el subarreglo derecho.

Y nuevamente llamamos a partitioning.

Implementación del algoritmo de clasificación rápida

A continuación tenemos un programa C simple que implementa el algoritmo de clasificación rápida:

Análisis de complejidad de clasificación rápida

Para una matriz, en la que la partición conduce a subarreglos desequilibrados, hasta el punto en que en el lado izquierdo no hay elementos, con todos los elementos mayor que el pivote, por lo tanto en el lado derecho.

Y si continúan obteniendo subarreglos desequilibrados, entonces la ejecución El tiempo de ejecución es el peor de los casos, que es O(n2)

Donde, como si la partición condujera a subarreglos casi iguales, entonces el tiempo de ejecución es el mejor, con la complejidad del tiempo como O (n * log n).

Complejidad de tiempo en el peor de los casos: O (n2)

Complejidad de tiempo en el mejor caso: O (n * log n)

Complejidad de tiempo promedio: O (n * log n)

Complejidad espacial: O (n * log n)

Como sabemos ahora, si los subarreglos se producen después de la partición están desequilibrados, la clasificación rápida tardará más en finalizar. Si alguien sabe que elige el último índice como pivote todo el tiempo, puede proporcionarle intencionalmente una matriz que resultará en el peor tiempo de ejecución para una clasificación rápida.

Para evitar esto, puede elegir aleatoriamente elemento pivote también. No hará ninguna diferencia en el algoritmo, ya que todo lo que necesita hacer es elegir un elemento aleatorio de la matriz, intercambiarlo con el elemento en el último índice, convertirlo en el pivote y continuar con la clasificación rápida.

• El espacio requerido por la clasificación rápida es muy menor, solo se requiere O(n*log n) espacio adicional.
• La ordenación rápida no es una técnica de ordenación estable, por lo que puede cambiar la aparición de dos elementos similares en la lista durante la ordenación.

Ahora que hemos aprendido la ordenación rápida algoritmo, también puede consultar estos algoritmos de clasificación y sus aplicaciones:

• Ordenar por inserción
• Ordenar por selección
• Ordenar por burbujas
• Combinar ordenación
• Ordenar montón
• Ordenar contando