Sådan beregnes volumen

Beregning af volumen

Volumen måles i terninger (eller kubiske enheder).

Hvor mange terninger er der i dette rektangulære prisme (cuboid)?

Vi kan tælle terningerne, selvom det er hurtigere at tage længden, bredden og højden og bruge multiplikation. Det rektangulære prisme ovenfor har et volumen på 48 kubik enheder.

Volumenet af et rektangulært prisme er = længde x bredde x højde

Eksempler på beregning af arealet af et rektangel

Vi skal udføre to multiplikationer for at finde ud af lydstyrken. Vi beregner arealet af det ene ansigt (eller siden) og gang det med dets højde. Eksemplerne nedenfor viser, hvordan der er tre måder at gøre dette på.

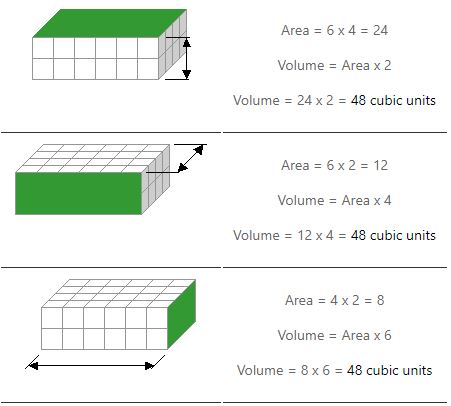
Læg mærke til, hvordan vi får det samme svar, uanset hvilken side vi bruger til at finde et område.

Når dit barn begynder at arbejde med areal og omkreds, vil han eller hun normalt arbejde med 2 dimensioner – firkanter, rektangler, trekanter osv., der vises på papir som flade – der er ingen dybde eller 3. dimension. Arbejde med volumen involverer 3 dimensioner. Sørg for, at dit barn er opmærksom på dette og ikke tænker på terningerne og andre 3D-figurer, der vises på papir, som bare en anden “form på siden”. Vis dem rigtige kasser, og vis hvordan disse kan tegnes (eller repræsenteres) på et todimensionelt stykke papir. Med andre ord skal du sørge for, at forbindelsen mellem hvad der står på papiret og hvad det repræsenterer i den virkelige verden er skabt. .

Enheder til måling af volumen

Der er meget store forskelle mellem måleenheder for volumen. For eksempel er der 100 centimeter i 1 meter, men der er 1.000.000 (ja, 1 million ) kubikcentimeter i en kubikmeter.

Hvorfor den store forskel? Fordi vi i volumen ikke kun har længde; vi har længde, bredde og højde. Eksemplet på sukkerterningen nedenfor viser dette.

Hvor meget sukker? 1 m3 eller 1.000.000 cm3

Tænk på at fylde en meget stor kasse (den ville være 1 meter bred, 1 meter, lang og en meter høj) med sukkerterninger (med hver side 1 centimeter).

	Trin 1: en række langs bunden af kassen – det ville være 100 sukkerterninger
	Trin 2: dæk resten af bunden af kassen – der giver i alt 100 rækker hver med 100 sukkerterninger. 100 x 100 = 10.000 sukker terninger i bunden af den store kasse.
	Trin 3: Gentag dette 99 gange, indtil der er lag med 10.000 terninger stablet 100 dybe. 10.000 x 100 = 1.000.000 sukkerter

Der er 1.000.000 cm3 i 1 m3 – pas på ikke at have for meget sukker!

Der er andre enheder til måling af volumen; kubikcentimeter, kubikfod, kubikmeter er alle enheder, der bruges til måling af volumen. Milliliter, liter, gallon bruges også især til måling af væsker.

Glem ikke wee 3

Vi skriver kubikstørrelser ved hjælp af en lille 3 ud for enheden.
Vi skriver mm3, cm3, m3, km3, cm3
Vi kan sige “85 centimeter kubik” eller “85 kubikcentimeter”

Eksempler på beregning af volumen af rektangulære prismer

	Volumen = Længde x Bredde x Højde Volumen = 12 cm x 8 cm x 6 cm = 576 cm3
	Volumen = Længde x Bredde x Højde Volumen = 20 mx 2 mx 2 m = 80 m3
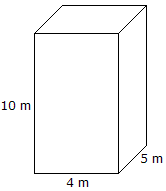	Volumen = Længde x Bredde x Højde volumen = 10 mx 4 mx 5 m = 200 m3

Cylinderens volumen

Beregning af volumenet af en cylinder der involverer multiplicering af basisarealet med cylinderens højde. Basen på en cylinder er cirkulær, og formlen for en cirkels areal er: areal af en cirkel = πr2. Der er mere her på området for en cirkel.

Volumen = Baseområde x Højde Volumen = πr2 xh Volumen = πr2 h

Bemærk: i nedenstående eksempler vi bruger 3.14 som en omtrentlig værdi for π (Pi).

Eksempel på beregning af volumen af en cylinder

Dimensionerne er i cm.

Volumen = πr2 h Volumen = 3.14 x 3 x 3 x 8 Volumen = 226,08 cm3

Volumen af en kegle

Volumenet af en kegle er lig med en tredjedel volumenet af en cylinder med matchende højde og basisareal. Dette giver formlen for volumen af en kegle som vist nedenfor.

Volumen = 1/3 πr2h

Eksempel på beregning af volumen af en kegle

Mål er i cm.

Volumen = 1/3 πr2 h Volumen = 1/3 x 3,14 x 2 x 2 x 7 Volumen = 29,31 cm3

Volumen af en sfære

Formlen for en kugles volumen er vist nedenfor.

Volumen = 4/3 πr3

Eksempel på beregning af volumenet af en sfære

Dimensionerne er i cm.

Volume = 4/3 πr3 Volume = 4/3 x 3,14 x 4 x 4 x 4 Volumen = 267,95 cm3

Arbejdsark, der kan udskrives

Brug regnearket nedenfor til at øve dig i at beregne volumener.

• Find volumen i kubiske enheder – rektangulære prismer kompositter
• Volumener af rektangulære prismer
• Volumener af rektangulære prismer
• Volumener af “virkelige” objekter f.eks. af kornkasser
• Beregning af volumener f.eks. af trekantede prismer og cylindre

Du får andre regneark med geometri på omkreds, areal og mere her.