Sådan beregnes areal
Beregning af areal
Areal måles i kvadrater (eller kvadratiske enheder).
Hvor mange kvadrater er der i dette rektangel?

Vi kan tælle firkanterne, ellers kan vi tage længden og bredden og brug multiplikation. Rektanglet ovenfor har et areal på 15 kvadrat enheder.
Arealet af et rektangel er = længde x bredde
Eksempler på beregning af arealet af et rektangel
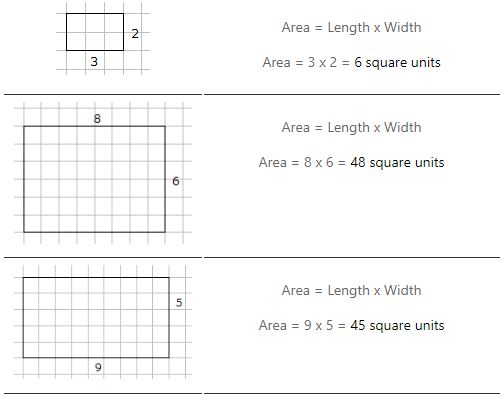
Enheder til måling af område
Vi måler areal ved hjælp af firkanter. Vi bruger forskellige størrelser af firkanter afhængigt af hvor stort eller lille et område er.
| Eksempel | Sidelængde på firkanter | Enhed |
| Størrelse på søm på tommelfingeren | Millimeter | mm2 |
| Papirstørrelse | Centimeter | cm2 |
| Størrelse på et rum | Meter | m2 |
| Bystørrelse | Kilometer | km2 |
Glem ikke wee 2
Vi skriver firkantede størrelser ved hjælp af en lille 2 ved siden af enheden.
Vi skriver mm2, cm2, m2, km2, cm2
Vi kan sige “63 millimeter i kvadrat” eller “63 kvadrat millimeter”
Vi kunne bruge små firkanter til at måle store områder. Det eneste problem med dette er, at vi ender med at bruge meget store numre. For eksempel kan et felt måles til 5.000.000.000 kvadratmillimeter, når 5.000 kvadratmeter ville have en meget lettere størrelse at sige, skrive og visualisere.
Du vil sandsynligvis høre flere enheder til måling af areal; kvadratcentimeter, kvadratfod, kvadratmeter, kvadratkilometer, acres, hektar er alle enheder, der bruges til at måle areal.
Flere eksempler på beregning af areal
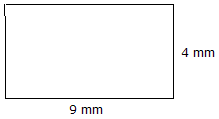 |
Areal = Længde x Bredde Areal = 9 mm x 4 mm = 36 mm2 |
 |
Areal = Længde x Bredde Areal = 7 cm x 6 cm = 42 cm2 |
 |
Areal = Længde x Bredde Areal = 8 mx 2 m = 16 m2 |
 |
Areal = Længde x Bredde Areal = 7 km x 5 km = 35 km2 |
Areal af en firkant
En firkantes længde og bredde er den samme, så vi skal bare gange længden med længden.
| Areal = Længde x Længde Areal = 6 cm x 6 cm = 36 cm2 |
Område af en cirkel
Området for en cirkel = πr2
hvor r er cirkelens radius, og π er forholdet mellem en cirkels omkreds og dens diameter.
π (udtales “pie” og ofte skrevet “Pi”) er en uendelig decimal med en fælles tilnærmelse til 3.14159. Du kan finde ud af mere om Pi her
Eksempel på beregning af en cirkels areal
 |
Area = πr2 Areal = 3.14159 x (4 cm) 2 Areal = 3.14159 x 16 cm2 Areal = 50.27 cm2 Svar afrundet til 2 decimaler |
Forklaring af området for en cirkelformel
Tag en cirkel og del den i lige store sektorer og omarrangere disse som vist nedenfor. Læg mærke til, hvordan formen bliver mere som et rektangel, når sektorerne bliver mindre. Bemærk: Der er ingen grænse for, hvor små disse sektorer kan være, og hvor tæt de kan ligne et rektangel, når de er arrangeret.
Forudsat at vi ved, at omkredsen af en cirkel er lig med 2πr, kan vi tilføje dimensioner til “rektanglet” som vist nedenfor. Ved hjælp af arealet af en formel for et rektangelareal, areal = bredde x højde kan vi se, hvordan vores cirkel, omkonfigureret som et rektangel, kan vises til at have et område, der svarer til πr xr eller πr2
Circle Sektorer omarrangeret

Cirkelsektorer omarrangeret – starter at ligne et rektangel

Område af Sammensatte former
Der er mange tilfælde, hvor beregningen af et samlet areal kræver, at mere end et område beregnes efterfulgt af enten en tilføjelse, en subtraktion eller en anden kombination af operationer for at finde det ønskede område.
Bemærk: I eksemplerne nedenfor vises måleenhederne ikke, og svarene og værdien af π (Pi) er afrundet til nærmeste hundrededel.
Eksempel: Enkle sammensatte former
Eksemplet på arealberegning nedenfor er relativt simpelt. Formen kan ses som en trekant kombineret med et rektangel.
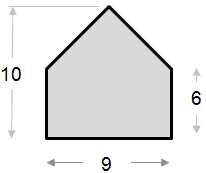 |
Areal af trekantdel: ½ x base x højde ½ x 9 x 4 = 18 Areal af rektangeldel: Samlet areal = 18 + 54 = 72 |
Eksemplet ovenfor illustrerer et fælles krav, når du arbejder med sammensatte figurer – finde dimensioner, der ikke vises. Når du underviser dine børn, skal du hjælpe, når det er nødvendigt, med at finde disse “manglende” dimensioner. Der er et andet eksempel nedenfor.
Find dimensionerne
 |
Hvad er dimensionerne på den lille rektangulære del? Bredde? 12 – 7 – 2 = 3 Højde? 8 – 6 = 2 |
Eksempel: Trække et område fra et andet
I eksemplet nedenfor kan formen ses som et rektangel med en udskåret trekant.
 |
Areal af rektangeldel: bredde x højde 5 x 6 = 30 Areal med trekantdel: Samlet areal = 30 – 4,50 = 25,50 |
Eksempel: Delområder
Eksemplet nedenfor ligner et ovenfor, men da vi har en halvcirkel, skal vi beregne en brøkdel (halvdelen) i cirkelens område. Bemærk i dette eksempel diameteren og ikke radius.
 |
Areal med trekantdel: ½ x base x højde ½ x 6 x 6 = 18 Areal med halvcirkeldel: Samlet areal = 18 – 3,53 = 14,47 |
Eksempel: Beslutninger! Forene? Træk
Det er almindeligt at have mere end én måde at beregne det endelige areal på. I eksemplerne nedenfor kan formen ses som to rektangler kombineret eller som et stort rektangel med et mindre rektangel “skåret ud” fra øverste højre hjørne.
Beregning af regneark
Udskriv ud nedenstående regneark og brug dem til praksis, når du underviser dine børn.
- Beregning af arealer – rektangler og firkanter
- Beregning af områder – rektangler
- Beregning Områder – rektangler
- Beregning af sammensatte områder f.eks med rektangulære former
- Beregning af sammensatte områder f.eks. med rektangler, trekanter og cirkler
- Beregning af områder f.eks. af trekanter
- Område af en cirkel
- Beregning af overfladearealer f.eks. af rektangulære prismer
Du finder flere regneark, der kan udskrives, her.