Poisson-distribution
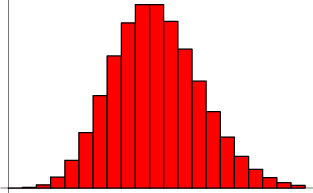
Givet en Poisson-proces, er sandsynligheden for at opnå nøjagtigt 
succeser i 
forsøg givet ved grænsen for en binomefordeling
 |
(1)
|
Visning af fordelingen som en funktion af det forventede antal succeser
 |
(2)
|
i stedet for prøvestørrelsen 
for fast 
bliver ligning (2) derefter
 |
(3)
|
Lad prøvestørrelsen 
blive stor, fordelingen nærmer sig derefter
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
som er kendt som Poisson-distributionen (Papoulis 1984, s. 101 og 554; Pfeiffer og Schum 1973, s. 200). Bemærk, at stikprøvestørrelsen 
er helt udgået af sandsynlighedsfunktionen, som har den samme funktionelle form for alle værdier af 
.
Poisson-fordelingen implementeres i WolframLanguage som PoissonDistribution.
Som forventet normaliseres Poisson-fordelingen, så summen af sandsynligheder er lig med 1, da
 |
(9 )
|
Forholdet mellem sandsynligheder er givet ved
 |
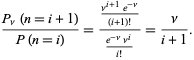(10)
|
Poisson-fordelingen når et maksimum når
 |
(11)
|
hvor er Euler-Mascheroni-konstanten og 
er et harmonisk tal, der fører til den transcendentale ligning
 |
(12)
|
som ikke kan løses nøjagtigt til 
.
Den moment-genererende funktion af Poissonsfordelingen gives af
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
så
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, s. 554).
De rå øjeblikke kan også beregnes direkte ved summering, hvilket giver en uventet forbindelse med Bell-polynomet 
og Stirling-numre af den anden slags,
 |
(21)
|
kendt som Dobińskis formel.Derfor
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
De centrale øjeblikke kan derefter beregnes som
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
så middelværdien, variansen, skævheden og kurtosisoverskuddet er
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
Den karakteristiske funktion for Poissondistribution er
(Papoulis 1984, s. 154 og 554), og kumuleringsgenereringsfunktionen er
 |
(34)
|
så
 |
(35)
|
Den gennemsnitlige afvigelse af Poisson-distributionen er givet ved
 |
(36)
|
Poisson-fordelingen kan også udtrykkes som
 |
(37)
|
 |
(38)
|
Den momentgenererende funktion af aPoisson-fordeling i to variabler er givet af
 |
(39)
|
Hvis de uafhængige variabler 
, 
, …, 
har Poisson-distributioner med parametre 
, 
, …, 
, derefter
 |
(40)
|
har en Poisson-fordeling med parameter
 |
(41)
|
Dette kan ses, da kumuleringsgenereringsfunktionen er
 |
(42)
|
 |
(43)
|
En generalisering af Poisson-fordelingen er blevet brugt af Saslaw (1989) til model den observerede klynge af galakser i universet. Formen på denne fordeling er givet af
 |
(44)
|
hvor 
er antallet af galakser i et volumen 
, 
, 
er den gennemsnitlige tæthed af galakser, og 
, med 
er forholdet mellem tyngdekraften og den kinetiske energi af mærkelige bevægelser, at lade 
giver
 |
(45)
|
hvilket faktisk er en Poisson-fordeling med 
. Ligeledes giver 
.