Måling: Opdag formler for område

Arealformler

Studerende, der har den uformelle forestilling om, at området er “mængden af 2-D ting “indeholdt i en region kan selv opfinde de fleste af de formler, som de ofte kun bliver bedt om at huske. Hver formel, de genopfinder, hjælper med at styrke deres forståelse (og hukommelse) for de andre formler, de kender. (Se også overfladeareal.)

Areal af rektangler

Ved at vælge en firkant som enhed af arealet får vi en intuitiv idé om arealet af rektangler. Hvis vi beslutter, at arealet af denne firkant er 1, så ville et rektangel , der er 7 gange så langt, have 7 × 1 som sit areal.

Et rektangel, der er dobbelt så højt som , vil have dobbelt så stort areal, så området for er 2 × 7 enheder. Vi kan tælle de to rækker på syv firkanter. Tilsvarende har 3 rækker med 7 firkanter (eller 7 søjler med 3 firkanter), i alt 7 × 3 firkanter, så dets areal er 21 kvadrat enheder.

Antallet af firkanter i en række er længden af rektanglet. Antallet af rækker er rektanglets højde. Så området er længde × højde.

Da et rektangel kan tegnes i en skråstilling, defineres “højde” til at betyde “retningen vinkelret på basen” og “base” er defineret til at være, uanset hvilken side du vælger at være.

Det fungerer for at tælle tal. Det fungerer endda for brøker. 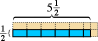Det blå rektangel, der vises her, måler halvdelen længde-enhed høj med fem og en halv længde-enheder bred. Hvis vi vælger den tilsvarende firkant som vores area-enhed, ser vi, at det blå rektangel indeholder fem halv-enheder areal og en fjerdedel-enhed areal, eller et i alt to og tre fjerdedelseenheder. (De lyserøde dele viser færdiggørelsen af hver kvadratareaenhed.)

For at inkludere alle tal definerer vi arealet af et rektangel til at være base × højde (hvor “base” og “højde” betyder længden af disse sider målt i de samme enheder).

Areal af parallelogrammer

Få idéen

Vi kan finde ud af en formel for arealet af et parallelogram ved dissekering at parallelogrammet og omarrangere delene for at skabe et rektangel. Fordi parallelogrammet og rektanglet er sammensat af de samme dele, har de nødvendigvis det samme område. (Se definitionen af område for mere om, hvorfor disse områder er ens.)

Vi kan se, at de også har nøjagtig samme bundlængde (blå) og nøjagtig samme højde (grøn). Da base × højde giver arealet af rektanglet, kan vi bruge de samme målinger på parallelogrammet til at beregne dets areal: base × højde. (Som før måles “højde” vinkelret på basen, og “base” er den side, du vælger først. Se parallelogram.)

Skåret vist ovenfor gør det let at se, at bundlængden er uændret. Faktisk kan den vinkelrette snit foretages hvor som helst langs bunden.

Afstivning af hullerne

Intuition og bevis

Denne dissektion giver en intuitiv forståelse af områdeformlen for et parallelogram, en grund til at det skal være, hvad det er. Men vi har ikke stillet spørgsmålstegn ved, om dissektionen virkelig “fungerer”. Når vi klipper parallelogrammet og omarrangerer dets dele, forventer vi at få , og resultatet ser bestemt sådan ud. Men udseende kan være vildledende. Hvad forsikrer os om, at når vi bevæger den trekant, er resultatet et rektangel? Hvad hvis det er mere som (dog mindre overdrevet)? Hvis resultatet ikke er altid et perfekt rektangel, vi kan ikke bruge vores viden om rektangelets områdeformel til at udvikle en formel til parallelogrammet. I gymnasiet vil eleverne være i stand til at bevise, at de to dele af parallelogrammet, når de samles ordentligt, laver et rektangel . I lønklasse K-8 skal eleverne for det meste stole på det visuelle eksperiment og få en intuitiv fornemmelse. Lær mere om, hvorfor disse dissektioner fungerer.

Hvad hvis vi vælger den korte side for at være basen?

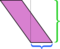
Vi kan frit vælge hvilken som helst side som base; “højde” er defineret til at være målt vinkelret på den side, vi vælger som base. Hvis vi tager den korte side (blå) som base, er dissektionen vist ovenfor ikke så overbevisende. At skære langs denne højde og omarrangere delene efterlader et rod:

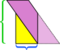
I dette særlige eksempel, vi kan redde rodet ved at lave endnu et snit, 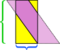men hvad nu hvis parallelogrammet var endnu længere og tyndere?

Det viser sig, at ethvert parallelogram, uanset hvor lang og tynd, kan dissekeres på denne måde, så delene – måske mange af dem – kan arrangeres i et rektangel. Men det kræver mere arbejde at vise, at dette altid kan gøres. Vi har brug for en anden idé.

En lidt anden dissektionside gør livet meget lettere i dette tilfælde. (På egen hånd kan du vise, at det også fungerer i den originale sag.)

• Læg parallelogrammet i et rektangel.
• De to dele af rektanglet, der ikke er inden for parallelogrammet, er kongruente trekanter.
• Skub en af disse trekanter mod den anden, indtil de mødes for at danne et rektangel. 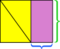Fordi det samlede areal af det udvendige rektangel ikke er ændret (det er det samme rektangel som før), og det gule område ikke har ændret sig (stykkerne lige flyttet rundt), forskellen mellem dem – de lilla områder – skal være de samme. Som før kan vi også se, at dimensionerne på det rektangulære lilla område er basen og højden af det originale parallelogram.

Intuition og bevis, reprise : Igen giver dissektionen den væsentlige indsigt, men det tager lidt mere arbejde at sikre, at de to gule trekanter, der bestemt ser ud som om de passer sammen for at skabe et rektangel, virkelig passer præcist og ikke bare næsten.

Hvorfor er det vigtigt at være så forsigtig?

Når vi bygger andre områdeformler (nedenfor), vil vi bruge vores hvordan man finder arealet af et parallelogram, og så ønsker vi at kunne stole på den regel, vi har fundet. Vi kan være sikre på, at omorganisering af dele ikke ændrer området: det er jo, hvordan vi definerer område. Men vi skal også være sikre på, at delene passer sammen, som vi hævder, at de gør, eller vi kan ikke stole på de målinger, vi har foretaget. Og vi skal være sikre på, at basen × højdereglen ikke afhænger af et heldigt valg af base.

I de fleste læseplaner har eleverne ikke en systematisk tilstrækkelig base af geometrisk viden før 8. klasse lyd bevis på, at disse dissektioner fungerer. Men den intuitive forståelse er nok til at forklare og retfærdiggøre formlerne og en god forankring for senere geometrisk undersøgelse.

Område med trekant

At vide, hvordan man finder arealet af et parallelogram, hjælper os find arealet af en trekant.

Dissekvering af trekanten

Vi kan dissekere trekanten i to dele – en af dem en trekant og en af dem en trapesformet – ved at skære den parallelt til basen. Hvis vi skærer højden nøjagtigt i halvdelen med denne skive, passer de to dele sammen for at lave et parallelogram med samme base men halvdelen af højden.

Så base × halv højde giver arealet af trekanten. En lignende dissektion viser halv base × højde. En af dem reduceres til bh.

Fordobling af trekanten og halvering af det resulterende område

En anden måde at tænke på: to kopier af trekanten laver et parallelogram med samme base og samme højde som trekanten.

Parallelogramets areal er base × højde, men det er dobbelt så stort som arealet af trekanten, så trekantsarealet er af base × højde, som vi så med dissektionsmetoden.

(Som altid skal du vælge en “base” og måle højden vinkelret på den base, fra basen til det modsatte toppunkt.)

Areal af trapezoid

Fordobling af trapezformet og halvering af det resulterende område

Som det var tilfældet med trekanten, kan to kopier af en trapez passer sammen for at skabe et parallelogram.

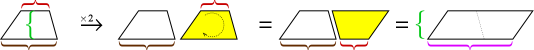
Højden af parallelogrammet er den samme som trapezens højde, men dens base er summen af trapezens to baser. Så parallelogrammets areal er højde × (base1 + base2). Men dette område er to trapezoider, så vi er nødt til at skære det i halve for at få arealet af trapezoidet.

Dissekering af trapezoidet

Vi kunne også dissekere trapezoidet, som vi dissekerede trekanten med et enkelt stykke, der skærer højden i halvdelen. De to dele passer sammen for at fremstille et parallelogram, hvis base er summen af trapezformens to baser, men hvis højde er halvt trapezhøjden.

I tilfælde af trapezoid kan baserne ikke vælges efter ønske. De to parallelle sider er baserne, og højden er som altid den lodrette afstand fra en base til det modsatte.

Arealet af dette parallelogram er dets højde (trapezens halvhøjde) gange dets base (summen af trapezformens baser), så dets areal er halvhøjde × (base1 + base2). Fordi parallelogrammet er lavet af nøjagtigt de samme “ting” som trapezformen, er det også området med trapezformet.

Uanset hvad er arealet af trapezformet × højde × (base1 + base2).

Område for andre specielle firkanter

Rhombusareal

Området for en rombe kan findes ved at skære og omarrangere stykkerne for at danne et parallelogram. Dette kan gøres på flere måder:

1. Skær tværs over den kortere diagonal (a) for at danne to kongruente trekanter. Flyt den nederste halvdel af trekanten ved siden af den øverste halvdel for at danne et parallelogram. Den kortere diagonal (a) bliver bunden af parallelogrammet, og halvdelen af den længere diagonal (b) bliver parallelogrammet. Området for romben er således et * b eller produktet af diagonalerne, hvilket er standardformlen for rhombus.
2. En anden lignende måde er at skære romben i fire kongruente trekanter og omarrangere dem til et rektangel med den kortere diagonal som basen og halvdelen længere diagonal som højden.
3. Efter skæring romben i to kongruente trekanter, vi kan beregne arealet af en af trekanten, som er * base (a) * højde ( b) = ab. Multiplicer derefter med to, da der er to af dem: 2 * ab = ab.

Drageområde

Dragenes område kan findes svarende til en rhombus. At skære over den længere diagonale giver to kongruente trekanter. Hvis vi omarrangerer dem, kan vi danne et parallelogram med den længere diagonal (b) som base og halvdelen af den kortere diagonal (a) som højden. Så området bliver b * a = ab. En mere kompliceret tilgang involverer lidt algebra. Skær dragen over den kortere diagonal for at danne to trekanter med den kortere diagonal (a) som base. Således er arealet af den første trekant a * skævt, hvor skævt er højden. Arealet af den anden trekant er a * (b – squiggly), hvor (b – squiggly) er den resterende del af den længere diagonale. Det samlede areal bliver således ( a * squiggly) + ( a * (b – squiggly)). Faktorering af a, vi har a (squiggly + b – squiggly) = ab.

Nå, hvad ved du. Dybest set behøver du kun at kende formlen for området for et parallelogram og derefter udlede formlen for de andre.