Eksponentiel fordeling
af Marco Taboga, ph.d.
Den eksponentielle fordeling er en kontinuerlig sandsynlighedsfordeling, der bruges til modeller den tid, vi har brug for at vente, før en given begivenhed finder sted. Det er den kontinuerlige modstykke til den geometriske fordeling, som i stedet er diskret.
Nogle gange kaldes det også negativ eksponentiel fordeling.
Introduktion
Hvor lang tid vil der gå, før et jordskælv opstår i et givet område? Hvor længe har vi brug for at vente, indtil en kunde kommer ind i vores butik? Hvor lang tid tager det, før et callcenter modtager det næste telefonopkald? Hvor længe vil et stykke maskine arbejde uden at gå i stykker?
Spørgsmål som disse besvares ofte i sandsynlige termer ved hjælp af den eksponentielle fordeling.
Alle disse spørgsmål vedrører den tid, vi har brug for at vente, før en given begivenhed finder sted. Hvis denne ventetid er ukendt, er det ofte hensigtsmæssigt at tænke på det som en tilfældig variabel, der har en eksponentiel fordeling.
Groft sagt, tiden 
at vente, før en begivenhed opstår, har en eksponentiel fordeling, hvis sandsynligheden for, at begivenheden finder sted i et bestemt tidsinterval, er proportional med længden af det tidsinterval.
Mere præcist, har en eksponentiel fordeling, hvis den betingede sandsynlighed er omtrent proportional med længden for tidsintervallet mellem tidene og , til enhver tid .
I mange praktiske situationer er denne egenskab meget realistisk. Dette er grunden til, at den eksponentielle fordeling er så udbredt til at modellere ventetider.
Den eksponentielle fordeling er strengt relateret til Poisson-distributionen. Hvis 1) en begivenhed kan forekomme mere end en gang og 2) den forløbne tid mellem to på hinanden følgende forekomster er eksponentielt fordelt og uafhængig af tidligere forekomster, så har antallet af forekomster af begivenheden inden for en given tidsenhed en Poisson-fordeling. Vi inviterer læseren til at se foredraget om Poisson-distributionen for en mere detaljeret forklaring og en intuitiv grafisk gengivelse af denne kendsgerning.
Definition
Den eksponentielle fordeling er karakteriseret som følger.
Definition Lad være en kontinuerlig tilfældig variabel. Lad dens støtte være sættet med positive reelle tal: Lad . Vi siger, at har en eksponentiel fordeling med parameter hvis og kun hvis dens sandsynlighedsdensitetsfunktion er Parameteren kaldes satsparameter.
En tilfældig variabel med en eksponentiel fordeling kaldes også en eksponentiel tilfældig variabel.
Det følgende er et bevis på, at er en legitim sandsynlighedsdensitetsfunktion.
Ikke-negativitet er indlysende. Vi er nødt til at bevise, at integralen af over er lig med . Dette bevises som følger:
For bedre at forstå den eksponentielle fordeling kan du se på dens densitetsdiagrammer.
Hastighedsparameteren og dens fortolkning
Vi har nævnt, at sandsynligheden for, at begivenheden finder sted mellem to datoer og er proportional med (betinget af, at den ikke er sket før ). Hastighedsparameteren er proportionalitetskonstanten: hvor er uendeligt stort af højere orden end (dvs. en funktion af , der går til nul hurtigere end gør).
Ovenstående proportionalitetsbetingelse er også tilstrækkelig til fuldstændigt at karakterisere den eksponentielle fordeling.
Proposition Proportionalitetsbetingelsen opfyldes kun, hvis har en eksponentiel fordeling.
Den betingede sandsynlighed kan skrives som 
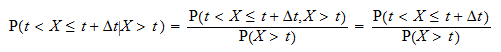Betegn ved fordelingsfunktionen for , dvs. og ved dets overlevelsesfunktion: Derefter Dele begge sider efter , vi får hvor er en mængde, der har tendens til når har tendens til . Ved at tage grænser på begge sider opnår vi eller ved definitionen af derivat: Denne differentialligning kan let løses ved hjælp af kæden regel: At tage integralet fra til på begge sider, får vi og eller Men (fordi ikke kan tage negative værdier) antyder Eksponererende begge sider, får vi Derfor eller Men densitetsfunktionen er den første afledte af fordelingsfunktionen: og udtrykket længst til højre er tætheden af en eksponentiel tilfældig variabel. Derfor er proportionalitetsbetingelsen kun opfyldt, hvis er en eksponentiel tilfældig variabel
Forventet værdi
Den forventede værdi af en eksponentiel tilfældig variabel er
Det kan afledes som følger: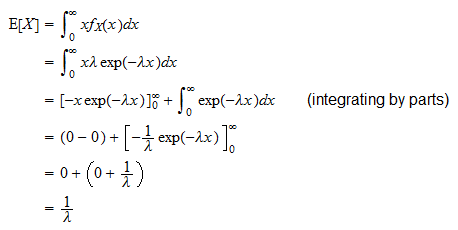 
Varians
Variansen af en eksponentiel tilfældig variabel er
It kan udledes takket være den sædvanlige variansformel (): 
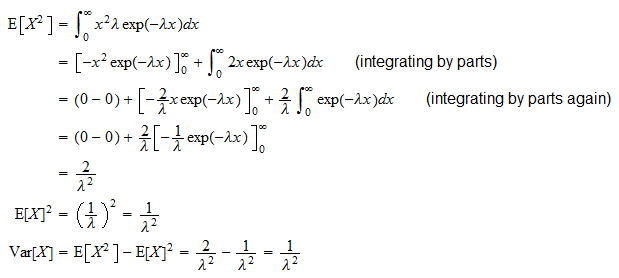
Momentgenererende funktion
Den øjeblikgenererende funktion af en eksponentiel tilfældig variabel er defineret for enhver :
Definitionen af momentgenererende funktion giver Af Selvfølgelig konvergerer ovenstående integraler kun, hvis , dvs. kun hvis . Derfor eksisterer øjeblikkets genereringsfunktionen for en eksponentiel tilfældig variabel for alle .
Karakteristisk funktion
Den karakteristiske funktion af en eksponentiel tilfældig variabel er
Ved at bruge definitionen af karakteristisk funktion og det faktum, at kan vi skrive Vi beregner nu de to integraler separat . Den første integral er 
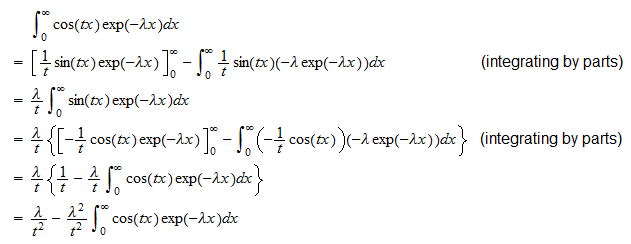Derfor som kan omarrangeres til at give eller Den anden integral er 
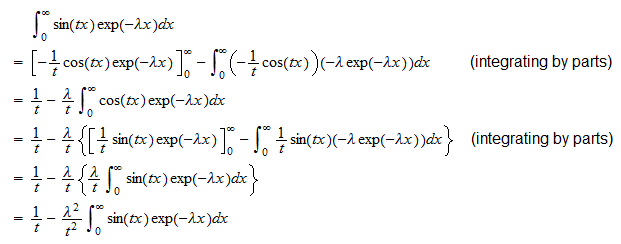Derfor som kan omarrangeres til at give eller Ved at sætte stykker sammen får vi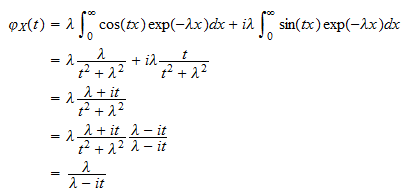 
Distributionsfunktion
Distributionsfunktionen for en eksponentiel tilfældig variabel er
Hvis , så fordi kan ikke påtage sig negative værdier. Hvis , så
Flere detaljer
I de følgende underafsnit kan du finde flere detaljer om den eksponentielle fordeling.
Hukommelsesløs egenskab
En af de vigtigste egenskaber ved den eksponentielle distribution er den hukommelsesløse egenskab: for enhver .
Dette bevises som følger: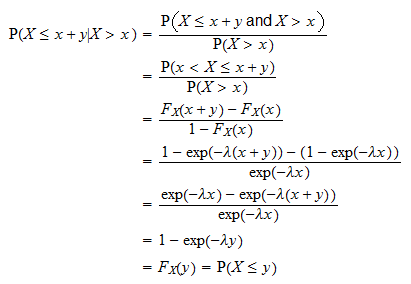 
er den tid, vi har brug for at vente, før en bestemt begivenhed opstår. Ovenstående egenskab siger, at sandsynligheden for, at begivenheden sker i et tidsinterval med en længde , er uafhængig af, hvor meget tid der allerede er gået () uden at begivenheden sker.
Summen af eksponentielle tilfældige variabler er en Gamma-tilfældig variabel
Antag , , …, er gensidigt uafhængige tilfældige variabler, der har eksponentiel fordeling med parameter .
Definer
Derefter er summen en Gamma-tilfældig variabel med parametre og .
Dette bevises ved hjælp af moment genereringsfunktioner (husk, at det øjebliksgenererende funktion af en sum af gensidigt uafhængige tilfældige variabler kun er produktet af deres øjeblikkeligt genererende funktioner): Sidstnævnte er det øjeblikgenererende funktion af en Gamma distribution med parametre og . Så har en gammafordeling, fordi to tilfældige variabler har den samme fordeling, når de har samme momentgenererende funktion.
Den tilfældige variabel siges også undertiden at have en Erlang-fordeling. Erlang-fordelingen er bare et specielt tilfælde af gammafordelingen: en gammal tilfældig variabel er også en Erlang-tilfældig variabel, når den kan skrives som en sum af eksponentielle tilfældige variabler.
Densitetsplot
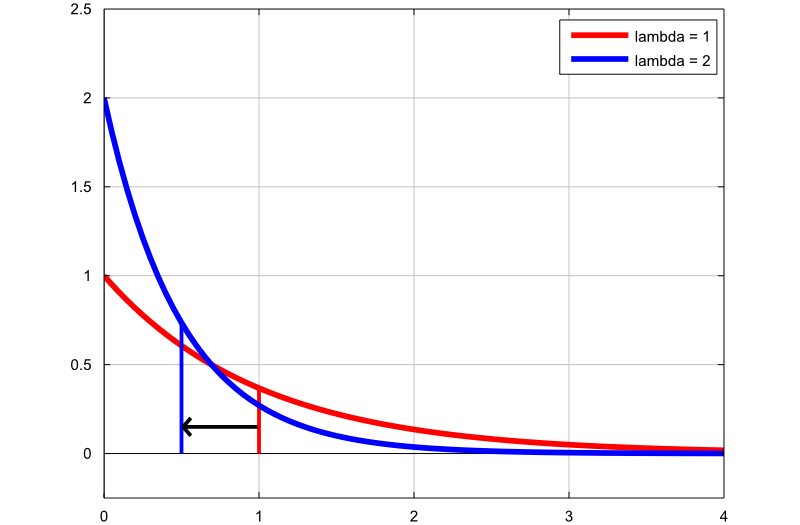
Det næste plot viser, hvordan densiteten af den eksponentielle fordeling ændres ved at ændre hastighedsparameteren:
-
den første graf (rød linje) er sandsynlighedsdensitetsfunktionen for en eksponentiel tilfældig variabel med satsparameter
; -
den anden graf (blå linje) er sandsynlighedsdensitetsfunktionen for en eksponentiel tilfældig variabel med hastighedsparameter
.
De tynde lodrette linjer angiver middelværdien af de to fordelinger. Bemærk, at ved at øge hastighedsparameteren reducerer vi gennemsnittet af fordelingen fra til .
Løst øvelser
Nedenfor kan du finde nogle øvelser med forklarede løsninger.
Øvelse 1
Lad være en eksponentiel tilfældig variabel med parameter . Beregn følgende sandsynlighed:
Først og fremmest kan vi skrive sandsynligheden som ved hjælp af det faktum, at sandsynligheden for, at en kontinuerlig tilfældig variabel får en bestemt værdi, er lig med nul (se Kontinuerlige tilfældige variabler og nul-sandsynlighedshændelser). Nu kan sandsynligheden skrives i form af fordelingsfunktionen for som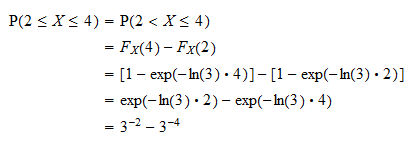 
Øvelse 2
Antag, at den tilfældige variabel har en eksponentiel fordeling med parameter . Beregn følgende sandsynlighed:
Denne sandsynlighed kan let beregnes ved hjælp af fordelingsfunktionen til :
Øvelse 3
Hvad er sandsynligheden for, at en tilfældig variabel er mindre end dens forventede værdi, hvis har en eksponentiel fordeling med parameter ?
Den forventede værdi af en eksponentiel tilfældig variabel med parameter er Sandsynligheden ovenfor kan beregnes ved hjælp af fordelingsfunktionen :
Sådan citeres
Citér venligst som: