College-algebra (Dansk)
Læringsresultater
- Identificer toppunktet, symmetriaksen, y-skæringspunktet og minimums- eller maksimumsværdien af en parabel fra det er en graf.
- Identificer en kvadratisk funktion, der er skrevet i generel og vertexform.
- Ved en kvadratisk funktion i generel form skal du finde toppunktet.
- Definer domænet og rækkevidde for en kvadratisk funktion ved at identificere toppunktet som et maksimum eller minimum.
Grafen for en kvadratisk funktion er en U-formet kurve kaldet en parabel. Et vigtigt træk ved grafen er, at den har et ekstremt punkt, kaldet toppunktet. Hvis parabolen åbner sig, repræsenterer toppunktet det laveste punkt på grafen eller minimumsværdien af den kvadratiske funktion. Hvis parabolen åbner sig, repræsenterer toppunktet det højeste punkt på grafen eller den maksimale værdi. I begge tilfælde er toppunktet et vendepunkt på grafen. Grafen er også symmetrisk med en lodret linje trukket gennem toppunktet, kaldet symmetriaksen.
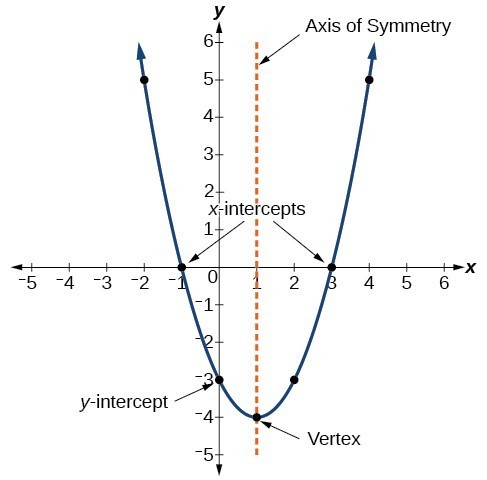
Ligninger af kvadratiske funktioner
Den generelle form for en kvadratisk funktion præsenterer funktionen i formen
f \ left (x \ right) = a {x} ^ {2} + bx + c
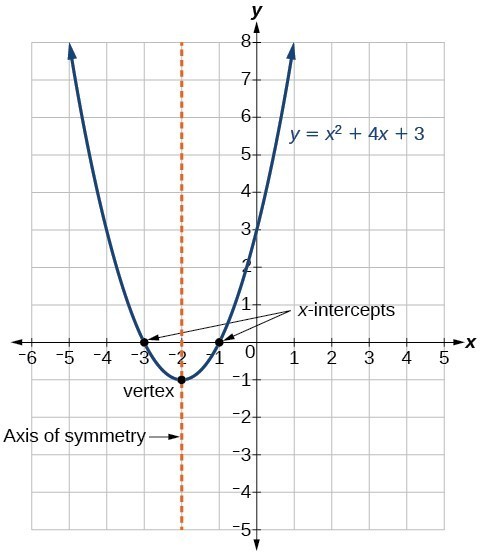
Standardformen for en kvadratisk funktion præsenterer funktionen i formen
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Givet generelt en kvadratisk funktion form, find parabelens toppunkt.
En af grundene til, at vi måske vil identificere parabelens toppunkt, er at dette punkt vil informere os om, hvor den maksimale eller minimale værdi af output forekommer, k, og hvor det sker, h. Hvis vi får den generelle form for en kvadratisk funktion:
f (x) = ax ^ 2 + bx + c
Vi kan definere toppunktet, (h, k), ved at gøre følgende:
Find domænet og rækkevidden for en kvadratisk funktion
Ethvert tal kan være inputværdien for en kvadratisk funktion. Derfor er domænet for enhver kvadratisk funktion alle reelle tal. Fordi paraboler har et maksimum eller et minimum ved toppunktet, er rækkevidden begrænset. Da toppunktet på en parabel vil være enten et maksimum eller et minimum, vil området bestå af alle y-værdier større end eller lig med y-koordinaten for toppunktet eller mindre end eller lig med y-koordinaten ved vendepunktet , afhængigt af om parabolen åbner eller ned.
Bidrag!
Forbedr denne sideFå flere oplysninger