College-algebra (Dansk)
Ved at se på grafen for en rationel funktion kan vi undersøge dens lokale adfærd og let se, om der er asymptoter. Vi kan endda være i stand til at tilnærme deres placering. Selv uden grafen kan vi dog stadig bestemme, om en given rationel funktion har nogen asymptoter, og beregne deres placering.
Vertikale asymptoter
De lodrette asymptoter for en rationel funktion kan være fundet ved at undersøge de faktorer i nævneren, der ikke er fælles for faktorerne i tælleren. Lodrette asymptoter forekommer ved nuller af sådanne faktorer.
Sådan: Givet en rationel funktion, identificer eventuelle lodrette asymptoter i dens graf.
- Faktor tælleren og nævner.
- Bemærk eventuelle begrænsninger i funktionens domæne.
- Reducer udtrykket ved at annullere fælles faktorer i tælleren og nævneren.
- Bemærk eventuelle værdier der får nævneren til at være nul i denne forenklede version. Dette er, hvor de lodrette asymptoter forekommer.
- Bemærk eventuelle begrænsninger i domænet, hvor asymptoter ikke forekommer. Disse er aftagelige diskontinuiteter.
Aftagelige diskontinuiteter
Lejlighedsvis vil en graf indeholde et hul: et enkelt punkt, hvor grafen ikke er defineret, angivet med en åben cirkel. Vi kalder et sådant hul for en flytbar diskontinuitet.
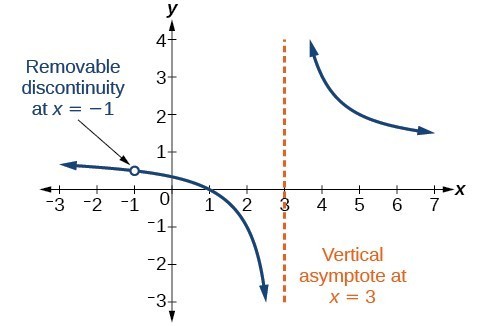
Figur 10
En generel note: Aftagelige diskontinuiteter af rationelle funktioner
En flytbar diskontinuitet forekommer i grafen for en rationel funktion ved x = a hvis a er et nul for en faktor i nævneren, der er fælles med en faktor i tælleren. Vi faktorerer tælleren og nævneren og kontrollerer for fælles faktorer. Hvis vi finder nogen, sætter vi den fælles faktor lig med 0 og løser. Dette er placeringen af den aftagelige diskontinuitet. Dette er sandt, hvis mangfoldigheden af denne faktor er større end eller lig med nævneren. Hvis mangfoldigheden af denne faktor er større i nævneren, er der stadig en asymptote ved denne værdi.
Horisontale asymptoter
Mens lodrette asymptoter beskriver en adfærd graf, da output bliver meget stort eller meget lille, vandrette asymptoter hjælper med at beskrive en grafs opførsel, da input bliver meget stor eller meget lille. Husk, at et polynomers slutadfærd vil afspejle den for det ledende udtryk. Ligeledes vil en rationel funktions slutadfærd afspejle forholdet mellem de tæller- og nævnerfunktioners førende termer.
Der er tre forskellige resultater, når der kontrolleres for vandrette asymptoter:
Tilfælde 1: Hvis tællerens grad > grad af tæller, er der en vandret asymptote ved y = 0.

Tilfælde 2: Hvis graden af nævneren < grad af tæller én, får vi en skrå asymptote.

Bemærk, at mens grafen for en rationel funktion aldrig vil krydse en lodret asymptote, grafen krydser måske eller ikke en vandret eller skrå asymptote. Selvom grafen for en rationel funktion kan have mange lodrette asymptoter, vil grafen højst have en vandret (eller skrå) asymptote.
Det skal bemærkes, at hvis graden af tælleren er større end graden af nævneren med mere end en, vil slutadfærden af grafen efterligne opførelsen af den reducerede slutadfærdsfraktion. For eksempel, hvis vi havde funktionen
med slutadfærd
grafens slutadfærd vil se ud som en jævn polynom med en positiv ledende koefficient.
En generel note: Horisontale asymptoter af Rationelle funktioner
Den rationelle funktions vandrette asymptote kan bestemmes ved at se på graderne på tælleren og nævneren.
- Tællergrad er mindre end graden af nævneren: vandret asymptote ved y = 0.
- Tællergraden er større end nævneren med én: ingen vandret asymptote; skrå asymptote.
- Tællergraden er lig med nævneren: vandret asymptote i forholdet mellem de førende koefficienter.
En generel note: Aflytninger af rationelle funktioner
En rationel funktion har en y-skæring, når input er nul, hvis funktion er defineret som nul. En rationel funktion har ikke en y-skæring, hvis funktionen ikke er defineret som nul.
Ligeledes vil en rationel funktion have x-aflytninger ved indgangene, der får output til at være nul. Da en brøkdel kun er lig med nul, når tælleren er nul, kan x-aflytninger kun forekomme, når tælleren for den rationelle funktion er lig med nul.
Prøv det 7
I betragtning af den gensidige kvadrerede funktion, der forskydes til højre 3 enheder og ned 4 enheder, skriv dette som en rationel funktion. Find derefter x– og y-aflytningerne og de vandrette og lodrette asymptoter.
Løsning