BFS vs DFS: Kend forskellen

Hvad er BFS ?

BFS er en algoritme, der bruges til at tegne data eller søge i træ- eller traverseringsstrukturer. Algoritmen besøger og markerer effektivt alle nøgleknuderne i en graf på en nøjagtig måde i bredden.

Denne algoritme vælger en enkelt knude (start- eller kildepunkt) i en graf og besøger derefter alle knudepunkter, der støder op til den valgte knude. Når algoritmen besøger og markerer startknudepunktet, bevæger den sig mod de nærmeste ubesøgte noder og analyserer dem.

Når de er besøgt, markeres alle noder. Disse gentagelser fortsætter, indtil alle knudepunkterne i grafen er blevet besøgt og markeret. Den fulde form for BFS er den første søgning i bredde.

I denne BSF Vs. DFS binært træ tutorial, du vil lære:

• Hvad er BFS?
• Hvad er DFS?
• Eksempel på BFS
• Eksempel på DFS
• Forskel mellem BFS og DFS binært træ
• Anvendelser af BFS
• Anvendelser af DFS

Hvad er DFS?

DFS er en algoritme til at finde eller krydse grafer eller træer i dybde-retning. Udførelsen af algoritmen begynder ved rodknudepunktet og udforsker hver gren inden backtracking. Det bruger en stakkedatastruktur til at huske, få det efterfølgende toppunkt og starte en søgning, hver gang en blindgyde vises i enhver iteration. Den fulde form for DFS er dybde-første søgning.

Eksempel på BFS

I det følgende eksempel på DFS, vi har brugt graf med 6 hjørner.

Eksempel på BFS

Trin 1)

Du har en graf med syv tal fra 0 – 6.

Trin 2)

0 eller nul er markeret som en rodnode.

Trin 3)

0 er besøgt, markeret og indsat i kødatastrukturen.

Trin 4)

Resterende 0 tilstødende og ubesøgte noder besøges, markeres og indsættes i køen.

Trin 5)

Traverserende gentagelser gentages indtil alle noder er besøgt.

Eksempel på DFS

I det følgende eksempel på DFS har vi brugt en ikke-rettet graf med 5 hjørner.

Trin 1)

Vi er startet fra toppunkt 0. Algoritmen begynder med at placere den i den besøgte liste og samtidig placere alle dens tilstødende hjørner i dataene struktur kaldet stak.

Trin 2)

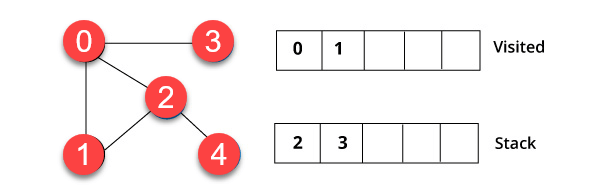
Du besøger elementet , som er øverst på stakken, for eksempel 1 og går til dens tilstødende noder. Det er fordi 0 allerede er besøgt. Derfor besøger vi toppunkt 2.

Trin 3)

Vertex 2 har et ubesøgt nærliggende toppunkt i 4. Derfor tilføjer vi det i stakken og besøger det.

Trin 4)

Endelig besøger vi det sidste toppunkt 3 har den ikke nogen ubesøgte tilstødende knudepunkter. Vi har afsluttet traverseringen af grafen ved hjælp af DFS-algoritme.

Forskel mellem BFS og DFS binært træ

BFS	DFS
BFS finder den korteste vej til destinationen.	DFS går til bunden af et undertræ, derefter backtracks .
Den fulde form for BFS er bredde-første søgning.	Den fulde form for DFS er dybde første søgning.
Den bruger en kø til at holde styr på den næste placering, du skal besøge.	Den bruger en stak til at holde styr på den næste placering, du skal besøge.
BFS krydser efter træniveau.	DFS krydser efter trædybde.
Det implementeres ved hjælp af FI FO-liste.	Den implementeres ved hjælp af LIFO-listen.
Det kræver mere hukommelse sammenlignet med DFS.	Det kræver mindre hukommelse sammenlignet med BFS.
Denne algoritme giver den laveste sti-løsning.	Denne algoritme garanterer ikke den laveste sti-løsning.
Der er ikke behov for backtracking i BFS.	Der er et behov for backtracking i DFS.
Du kan aldrig blive fanget i endelige sløjfer.	Du kan blive fanget i uendelige sløjfer.
Hvis du ikke finder noget mål, skal du muligvis udvide mange noder, før løsningen findes.	Hvis du ikke finder noget mål, kan back-tracking af bladknudepunkter muligvis forekomme.

Anvendelser af BFS

Her er anvendelser af BFS:

Uvægtet Grafer:

BFS-algoritme kan nemt oprette den korteste sti og et minimum spændende træ for at besøge alle hjørnerne i grafen på den kortest mulige tid med høj nøjagtighed.

P2P-netværk:

BFS kan implementeres for at finde alle de nærmeste eller nærliggende noder i et peer-to-peer-netværk. Dette finder de krævede data hurtigere.

Webcrawlere:

Søgemaskiner eller webcrawlere kan nemt opbygge flere niveauer af indekser ved at anvende BFS. BFS-implementering starter fra kilden, som er websiden, og derefter besøger den alle links fra den kilde.

Netværksudsendelse:

En udsendt pakke styres af BFS-algoritmen til at finde og nå alle de noder, den har adressen til.

Anvendelser af DFS

Her er vigtige anvendelser af DFS:

Vægtet graf:

I en vægtet graf genererer DFS-graf traversal træet med den korteste sti og det mindst mulige træ.

Registrering af en cyklus i en graf:

En graf har en cyklus, hvis vi fandt en bagkant under DFS. Derfor skal vi køre DFS til grafen og kontrollere for bagkanter.

Find vej:

Vi kan specialisere os i DFS-algoritmen til at søge en sti mellem to hjørner.

Topologisk sortering:

Det bruges primært til planlægning af job fra de givne afhængigheder blandt jobgruppen. I datalogi bruges det til instruktionsplanlægning, dataserialisering, logisk syntese, bestemmelse af rækkefølgen af kompileringsopgaver.

Søgning efter stærkt forbundne komponenter i en graf:

Det bruges i DFS-graf, når der er en sti fra hvert toppunkt i grafen til andre tilbageværende toppunkter.

Løsning af gåder med kun én løsning:

DFS-algoritme kan let tilpasses til at søge i alle løsninger til en labyrint ved at inkludere noder på den eksisterende sti i det besøgte sæt.