Ruletové kurzy a pravděpodobnosti

Hra rulety láká miliony hráčů s příslibem rychlých a snadných zisků, pokud by se jejich šťastné číslo objevilo hned při dalším losování míče. Pravidla rulety se snadno ovládají, ale mnoho nezkušených hráčů nedokáže rozpoznat společný fakt, že čím je daná kasinová hra jednodušší, tím větší výhodu má dům oproti těm, kdo ji hrají. Totéž platí v plné síle pro lákavou hazardní hru, kterou je ruleta.

Tato hra nemusí vyžadovat, aby hráči byli matematickými géniové, přesto by bylo nemožné, aby se z dlouhodobého hlediska stali vítězi, aniž by získali správné pochopení pojmů, jako jsou šance a pravděpodobnosti. I když neexistuje žádný jistý způsob, jak by hráč rulety mohl správně předpovědět, jaké číslo by zasáhlo při příštím roztočení, alespoň základní znalost pravděpodobnosti a pravděpodobnosti vám může pomoci lépe se informovat při rozhodování o tom, které typy sázek na umístění. Pokud jste v této vzrušující hazardní hře noví, přečtěte si krátký úvod o tom, jak se na ruletu vztahují pojmy pravděpodobnosti a pravděpodobnosti.

Koncept pravděpodobnosti v ruletě

Než vystavíte riziku své vlastní prostředky a umístíte své první sázky na skutečné peníze na ruletu , musíte získat alespoň základní znalosti o tom, co znamená pravděpodobnost. Obecně se tento termín používá k označení pravděpodobnosti výskytu dané náhodné události. Uvedená pravděpodobnost je vyjádřena buď ve formě zlomků, nebo v procentech.

Pravděpodobnost výskytu náhodné události může být zobrazena na řádku a je jí přiřazena hodnota v rozmezí od 0 do 1, například 0 ______ 1 / 2______1. Na levé straně máme 0, což znamená, že náhodná událost je nemožná a jako taková se nikdy neuskuteční. Směrem ke středu pravděpodobnostní linie jsou šance na událost, které se vyskytnou, rovny nebo ½. Napravo máme 1, což znamená, že k náhodné události pravděpodobně dojde.

V ruletě je poměrně snadné určit pravděpodobnost výhry u konkrétních typů sázek. Jak víme, existuje buď 37 nebo 38 možných výsledků na jedno otočení, v závislosti na tom, zda hrajete na kole s jednou nulou nebo s dvojitou nulou. Vzhledem k tomu, že výsledky v ruletových hrách jsou zcela náhodné, existují pro hráče pouze dva možné výsledky – buď vyhrají, nebo prohrají.

Proto se pravděpodobnost výhry u daného typu sázky vypočítá vydělením počtu způsobů, jak vyhrát, celkovým počtem všech možných výsledků. Jiným způsobem, jak by se dalo říct, je, že pravděpodobnost výhry se rovná počtu způsobů, jak vyhrát, děleno součtem způsobů, jak vyhrát, a způsobů, jak prohrát.

Z toho vyplývá, že můžeme vypočítat pravděpodobnost výhry s danou ruletovou sázkou pomocí následujícího vzorce – Pravděpodobnost výhry = Způsoby výhry / (Způsoby výhry + Způsoby ztráty). Nejprve si ukážeme, jak to funguje, a jako příklad použijeme losování.

Jak víte, při házení mincí existují pouze dva možné výsledky, protože mince dopadne buď na hlavy, nebo na ocasy. Šance na přistání na obou stranách jsou prakticky stejné. Pomocí výše uvedeného vzorce bychom provedli následující výpočet: Pravděpodobnost hlav = 1/1 + 1 = 0,50. Abychom tento výsledek převedli na procento, vynásobíme 100 a získáme 50%.

Nyní použijeme vzorec shora a vypočítáme pravděpodobnost sbírání výplaty sázkou Split ve hře rulety. Vzhledem k tomu, že s Split sázkami hráči pokrývají pouze dvě čísla, která sousedí s rozložením, existují pouze dva způsoby, jak vyhrát z 37 možných výsledků, tj. Pokud jeden hraje na evropském kole s nulou. Dalším způsobem, jak by to bylo řečeno, jsou dva způsoby, jak vyhrát a 35 způsobů, jak prohrát sázkou na Split. Proto bude výpočet probíhat následovně: 2 / (2 + 35) = 0,0540 x 100 = 5,40%. Naproti tomu pravděpodobnost výhry se stejnou sázkou v americké ruletě klesne na 5,26%, což se shodou okolností shoduje s hranou hry ve hrách s dvojitou nulou.

Čím větší počet výsledků pokryjete jedinou sázkou, tím vyšší bude pravděpodobnost výhry. Předpokládejme například, že máte zájem experimentovat s jednou z exotičtějších ruletových sázek, jako je Voisin du Zero, která pokrývá sled sedmnácti náhodných čísel na kolečku s nulou. Pravděpodobnost zasažení jednoho z těchto výherních čísel se rovná 45,94% nebo 17 / (17 + 20) x 100, protože jednou takovou sázkou pokrýváte téměř polovinu celého kola. Jak pravděpodobně vidíte sami, zjištění pravděpodobnosti výhry s různými typy sázek na ruletu nevyžaduje hluboké matematické znalosti.

Kurzy sázek na ruletu

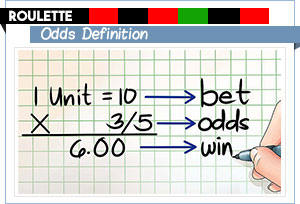Pravidla platná u kasinových stolů jsou navržena tak, aby byla nakloněna výhoda ve prospěch domu.Z tohoto důvodu je pro hráče rulety nesmírně důležité naučit se, jak vypočítat šance na výhru u každého typu sázky.

Někteří lidé mylně věří, že lze použít pojmy „šance“ a „pravděpodobnost“. zaměnitelně, i když ve skutečnosti nemohou, jednoduše proto, že označují dva různé pojmy. Pokud nejste obeznámeni s pojmem „šance“, znamená to poměr mezi počtem způsobů, jak vyhrát, a počtem způsobů, jak prohrát. Na rozdíl od pravděpodobnosti nejsou šance nikdy vyjádřeny v procentech, ale jsou obvykle prezentovány jako dvojice čísel.

Kurz na náhodnou událost, jako je losování nebo rotace rulety, označuje pravděpodobnost, že se tato událost odehraje. Chcete-li vypočítat šance na výhru s danou ruletovou sázkou, musíte zjistit, co jeho pravděpodobnost je. Pak můžete použít následující vzorec: Kurzy na výhru = Pravděpodobnost výhry / (1 – Pravděpodobnost výhry). Použijeme-li příklad převrácení mince shora, výpočet bude probíhat následovně: 0,5 / (1 – 0,5) = 1/1, což lze také vyjádřit jako 1: 1. Kurzy jsou v tomto případě sudé.

Existuje však jednodušší způsob, jak zjistit pravděpodobnost výhry sázkami na ruletu a to je jednoduše vydělit počet způsobů, jak vyhrát, počtem způsobů, jak prohrát. Proto je šance na výhru s postupkou rovnou Například t 32 Red bude vyjádřeno jako Kurz na výhru = 1/36 nebo 1 až 36, protože existuje pouze jedno výherní číslo a 36 čísel, které vedou ke ztrátě. Jak vidíte, pravděpodobnost se liší od pravděpodobnosti v tom, že se jedná o pravděpodobnost 1 z 37 výsledků. Podobně by šance na výhru sázkou Split z předchozího příkladu byla 2 až 35 nebo 2/35.

Někteří hráči rulety mají tendenci zaměňovat šance na výhru s pravděpodobností proti výhře, protože poměr je při mnoha příležitostech napsán obráceně, například 36: 1. To není úplně totéž, protože šance proti daná událost odráží pravděpodobnost, že se uvedená událost nestane. V tomto případě bude vzorec pro výpočet kurzů proti dané výhře sázky také obrácen takto: Kurzy proti výhře = způsoby ztráty / způsoby výhry. Proto je šance na výhru sázkou Straight Up na 32 Red rovna 36/1.

Tyto obrácené kurzy obvykle používají provozovny hazardních her k vypisování výplat výherních sázek. Čím menší je pravděpodobnost výhry s danou ruletovou sázkou, tím větší je návrat, který nabízí dům. Je tomu tak proto, že pokud jde o většinu kasinových her, včetně rulety, hráči prakticky soutěží proti domu. Dům proto sází proti svým patronům, takže zaplacené kurzy jsou kurzy proti výhře hráče, tedy převrácený poměr. Podrobnější informace týkající se domácích kurzů si budete moci přečíst v následující části.

Kurzy kasina a jak se odráží na ziskovosti hráčů

Pokud jde o kasinové hry, vždy existují rozdíly. mezi matematickou pravděpodobností výhry sázkami a poměrem, ve kterém jsou tyto sázky vypláceny. Právě tento rozdíl mezi skutečnými kurzy na výhru a kasinovými kurzy dává dlouhodobě výhodu domu nad hráči.

U každé hry, kterou kasino nabízí, jsou výplatní kurzy na sázky stanoveny tak, aby kasino mohlo generovat zisky z každé vaší sázky. Tato výhoda domu je vyjádřena v procentech, které odrážejí celkovou návratnost, kterou může kasino očekávat v průběhu času, nebo jinými slovy, průměrné procento hráčů nevyhnutelně z dlouhodobého hlediska ztratí. Protože je kasino komerční, potřebuje svoji výhodu, aby pokrylo náklady spojené s hostováním her. Sečteno a podtrženo, bez ohledu na to, jak malá je tato hrana, stále se může časem rozmělnit na bankrollu.

V některých hazardních hrách, jako jsou kostky, existují divoké výkyvy na okraji domu pro různé typy sázek . To neplatí pro ruletu, kde hrana zůstává konstantní, s jedinou výjimkou, kterou je sázka pěti čísel. Ten druhý může být vyroben pouze ve hrách s dvojitou nulou a dává domu výhodu 7,89%.

Pro výpočet okraje kasina v ruletě vynásobíme rozdíl mezi skutečnými kurzy proti výhře a kurzy v kasinu pravděpodobností výhry. Na kole s dvojitou nulou jsou šance na výhru sázkou Straight Up 37 ku 1, ale dům platí pouze 35 ku 1, což vede k okraji domu 5,26%. Jak vidíte, rozdíl mezi kurzy na výhru a výplatou v americké ruletě se rovná dvěma jednotkám. Pomocí vzorce shora můžeme vypočítat hranu domu takto:

(37/1 – 35/1) x 1/38 = 2/1 x 1/38 = 0,0526 x 100 = 5,26%

Okraj domu v evropské ruletě je výrazně menší, protože na kole je pouze jedna nulová kapsa, takže výpočet bude probíhat následovně:

(36/1 – 35/1) x 1/37 = 1/1 x 1/37 = 0,0270 x 100 = 2,70%.

Jinými slovy, hráči budou čelit ztrátám v průměru 27 GBP za každých 1 000 GBP, které vsadí na evropskou ruletu. Pamatujte, že takové ztráty můžete očekávat pouze po delší dobu, která zahrnuje desítky tisíc zatočení. Krátkodobě je možné vše, takže hráči mohou být určitě vpřed, pokud budou na ruletu rekreačně sázet jeden nebo dva dny.

Podobně šance na výhru sázkou Corner (která pokrývá čtyři sousední čísla na rozložení) jsou 33 až 4 na kole s jednou nulou, ale kasino vyplácí hráčům pouze 32 až 4, což znamená, že dům shromažďuje zisk jedné jednotky ze všech vítězných sázek na roh. V americké ruletě, kde jsou na kole dvě nuly, bude kasino na těchto sázkách profitovat se dvěma jednotkami, protože šance na výhru se dále zvyšují na 34 na 4, ale výplatní kurzy zůstávají 32 na 4.

V hazardních hrách, jako je ruleta, není možné uniknout z okraje domu – čím více hrajete, tím více z dlouhodobého hlediska ztratíte. To je důvod, proč variace rulety, kterou člověk hraje, má velký dopad na jejich celkovou dlouhodobou ziskovost. Dává smysl, že hra na kolečkách s jednou nulou je pro hráče výhodnější, zvláště pokud platí pravidla La Partage nebo En Prison, protože snižují výhodu kasina na 1,36%.

Výpočet kursů za po sobě jdoucí čísla

Někteří hráči dělají chybu, když shlukují dva nebo více po sobě jdoucích výsledků rulety a věří, že předchozí výhra čísla ovlivňují výsledky při následujících otočeních. Tito hráči mohou být svědky příchodu černé čtyřikrát po sobě a nesprávně předpokládat, že pravděpodobnost příchodu další červené je vyšší, protože míč na chvíli nepřistál na červené kapse.

Pravdou je, že tento způsob myšlení je nesprávný, protože pravděpodobnost výhry s jakýmkoli jednotlivým číslem je vždy stejná, bez ohledu na to, kolikrát za sebou toto číslo vyhrálo. Je však možné vypočítat kombinovanou pravděpodobnost výhry s danou sázkou rulety dvakrát, třikrát nebo vícekrát za sebou. Jako příklad si ukážeme sázku Straight Up na 9 červených v evropské ruletě, abychom ukázali, jak se to dělá.

Kombinovaná pravděpodobnost výhry s 9 červenými dvěma po sobě jdoucími časy je výsledkem znásobení jednotlivých pravděpodobností tohoto čísla nebo 1/37 x 1/37 = 1/1369. Pravděpodobnost výhry s 9 červenými klesá s každým dalším opakováním. Pravděpodobnost, že se toto jednotlivé číslo objeví třikrát za sebou, se tedy rovná 1/37 x 1/37 x 1/37 = 1/50653.

Pravděpodobnost výhry s 9 červenými na libovolném daném čísle rotace je vždy stejná nebo 1/37. Ale vítězství se stejným jednotlivcem číslo tři, čtyřikrát nebo vícekrát za sebou je evidentně vzácný výskyt. Jak vidíte z výše uvedeného výpočtu, trefení stejného čísla třikrát po sobě představuje 1 šanci z 50 653. To odpovídá 0,0019% šanci na výhru se stejným počtem třikrát po sobě.
Pamatujte, že opakování samotných výsledků rulety není tak vzácným jevem. Číslo se pravděpodobně opakuje v průměru jednou za každých 37 vrhnutí míče, což znamená, že 9 červených pravděpodobně zasáhne přibližně dvakrát za hodinu. Jedná se o po sobě jdoucí opakování čísla, které je vzácnou událostí.

Výpočet kurzů pro pruhy

K pruhům obvykle dochází u sázek se sudými penězi, kde jsou šance na výhru a prohru téměř stejné. V návaznosti na stejný způsob uvažování jako v předchozí části jsme zjistili, že pravděpodobnost výhry se sázkou s rovnoměrnými penězi na Black se rovná 18/37 na evropském kole, protože z 18 je 18 výherních kapes.

Pokud červená zasáhla třikrát po sobě, zůstává pravděpodobnost, že černá přijde další, 18/37. Totéž platí pro červené zasažení ve čtvrtém roztočení. Ve skutečnosti to platí pro každou sázku sudých peněz, ať už vysokou / nízkou, červenou / černou nebo lichou / sudou, protože pravděpodobnost každého z těchto výsledků je vždy 18/37 na kolečku s jednou nulou. Málo záleží na tom, jaký byl výsledek předchozího zatočení.

Pravděpodobnost výherní série u sázek se sudými penězi se počítá stejným způsobem jako u výher jednotlivých čísel několikrát za sebou. Jinými slovy, musíme znásobit jednotlivé pravděpodobnosti výsledku. Pravděpodobnost, že s Blackem zažijete dobrou sérii, když vyhrajete tři po sobě jdoucí časy, by se tedy rovnala 18/37 x 18/37 x 18/37 = 5832/50653 = 1 / 8,68. Proto je pravděpodobné, že k takovému pruhu dojde v průměru jednou za osm a půl hodu míčem.

Je také možné zjistit, jaká je pravděpodobnost série porážek. Vzhledem k tomu, že sázky se sudými penězi prohrávají vždy, když míč spadne do zelené nulové kapsy, je například pravděpodobnost prohry na černém 19/37 na evropském kole, protože existuje 19 způsobů, jak prohrát z 37 možných výsledků.Vzorec pro sérii porážek je stejný jako pro sérii vítězných. Pravděpodobnost prohry třikrát po sobě s Blackem je 19/37 x 19/37 x 19/37 = 6859/50653 = 1 / 7,38. To znamená, že v průměru zaznamenáte tři po sobě jdoucí ztráty sázkami s rovnoměrnými penězi jednou za každých 7,4.

• Americká ruleta
• Nejlepší ruletové stránky se skutečnými penězi
• Nejlepší ruletové systémy
• zdvojnásobení Action Roulette
• Double Ball Roulette
• Evropská ruleta
• Francouzská ruleta
• High Roller Roulette
• Nejoblíbenější ruleta Hry
• Hrajte ruletu online
• Progresivní jackpotová ruleta
• Sázky a vzory sázek na ruletu
• Pravidla rulety
• Ruleta Strategie
• Varianty rulety