Snabbsorteringsalgoritm

Snabbsortering är en av de olika sorteringsteknikerna som bygger på konceptet Divide and Conquer, precis som slå samman sortering. Men i snabb sortering görs alla tunga lyft (större arbeten) medan man delar upp matrisen i underarrangemang, medan i fall av sammanslagning sker allt verkligt arbete under sammanslagning av underarrangemang. Vid snabb sortering gör kombinationssteget absolut ingenting.

Det kallas också sorteringspartitionsutbyte. Denna algoritm delar listan i tre huvuddelar:

1. Element mindre än pivotelementet
2. Pivotelement (centralt element)
3. Element större än pivotelement

Pivotelement kan vara vilket element som helst från matrisen, det kan vara det första elementet, det sista elementet eller vilket slumpmässigt element som helst. I denna handledning tar vi elementet längst till höger eller det sista elementet som pivot.

Till exempel: I matrisen {52, 37, 63, 14, 17, 8, 6, 25} tar vi 25 som pivot. Så efter det första passet kommer listan att ändras så här.

{6 8 17 14 25 63 37 52}

Efter det första passet kommer därför svängen att ställas in på sin position, med alla element mindre till vänster och alla element större än till höger. Nu betraktas 6 8 17 14 och 63 37 52 som två separata soluppställningar, och samma rekursiva logik kommer att tillämpas på dem, och vi fortsätter att göra detta tills hela matrisen sorteras.

Hur fungerar snabb sortering?

Följande steg är involverade i snabb sorteringsalgoritm:

1. Efter att ha valt ett element som pivot, som är det sista indexet för arrayen i vårt fall, delar vi arrayen för första gången.
2. I snabb sortering kallar vi denna partitionering. Det är inte enkelt att dela upp arrayen i två subarrays, men vid partitionering är arrayelementen så placerade att alla element som är mindre än pivot kommer att vara på vänster sida av pivot och alla element större än pivot kommer vara på höger sida av det.
3. Och pivotelementet kommer att vara i sitt slutliga sorterade läge.
4. Elementen till vänster och höger kanske inte sorteras.
5. Sedan väljer vi underarrayer, element till vänster om pivot och element till höger om pivot, och vi utför partitionering på dem genom att välja en pivot i subarrays.

Låt oss betrakta en matris med värden {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Nedan har vi en bildrepresentation av hur snabb sortering kommer att sortera den givna matrisen.

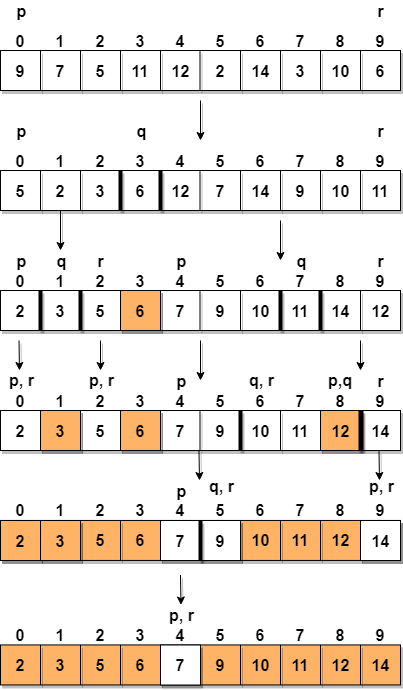
I steg 1 väljer vi det sista elementet som pivot, vilket är 6 i det här fallet, och kräver partitioning, därmed omarrangera g arrayen på ett sådant sätt att 6 kommer att placeras i sin slutliga position och till vänster kommer alla elementen att vara mindre än den och till höger kommer vi att ha alla element större än det.

Sedan väljer vi undergruppen till vänster och undergruppen till höger och väljer en led för dem, i ovanstående diagram valde vi 3 som pivot för vänster subarray och 11 som pivot för höger subarray.

Och vi uppmanar igen till partitioning.

Implementering av algoritm för snabb sortering

Nedan har vi ett enkelt C-program som implementerar algoritmen för snabb sortering:

Komplexitetsanalys av snabb sortering

För en matris där partitionering leder till obalanserade underarrayer, i en utsträckning där det inte finns några element på vänster sida med alla element större än svängningen, därav på höger sida.

Och om du fortsätter att få obalanserade underarrangemang, så kör ningstiden är det värsta fallet, det vill säga O(n2)

Var som om partitionering leder till nästan lika subarrays, då är körtiden den bästa, med tidskomplexitet som O (n * log n).

Komplexitet i värsta fall: O (n2)

Komplexitet i bästa fall: O (n * log n)

Genomsnittlig tidskomplexitet: O (n * log n)

Rymdkomplexitet: O (n * log n)

Som vi vet nu, att om subarrays partitionering produceras efter partitionering är obalanserade, tar snabb sortering mer tid att avsluta. Om någon vet att du väljer det sista indexet som pivot hela tiden, kan de medvetet förse dig med array som kommer att resultera i värsta fallets gångtid för snabb sortering.

För att undvika detta kan du välja pivotelement också. Det kommer inte att göra någon skillnad i algoritmen, eftersom allt du behöver göra är att välja ett slumpmässigt element från matrisen, byta ut det med elementet vid det sista indexet, göra det till pivot och fortsätta med snabb sortering.

• Utrymme som krävs med snabb sortering är mycket mindre, endast O(n*log n) ytterligare utrymme krävs.
• Snabbsortering är inte en stabil sorteringsteknik, så det kan ändra förekomsten av två liknande element i listan under sortering.

Nu när vi har lärt oss Snabbsortering algoritm kan du också kolla in dessa sorteringsalgoritmer och deras applikationer:

• Insättningssortering
• Urvalssortering
• Bubblesortering
• Sammanfoga sortering
• Högsortering
• Räkna sortering