Schnellsortierungsalgorithmus

Die Schnellsortierung ist eine der verschiedenen Sortiertechniken, die genau wie das Konzept von Teilen und Erobern basiert Zusammenführen, sortieren. Beim schnellen Sortieren wird jedoch das gesamte schwere Heben (Hauptarbeit) ausgeführt, während das Array in Subarrays unterteilt wird, während beim Zusammenführen der Sortierung die gesamte eigentliche Arbeit beim Zusammenführen der Subarrays erfolgt. Bei einer schnellen Sortierung führt der Kombinationsschritt absolut nichts aus.

Er wird auch als Partitionsaustausch-Sortierung bezeichnet. Dieser Algorithmus unterteilt die Liste in drei Hauptteile:

1. Elemente kleiner als das Pivot-Element
2. Pivot-Element (zentrales Element)
3. Elemente größer als das Pivot-Element

Pivot-Element kann ein beliebiges Element aus dem Array sein, es kann das erste Element, das letzte Element oder ein beliebiges zufälliges Element sein. In diesem Tutorial nehmen wir das Element ganz rechts oder das letzte Element als Drehpunkt.

Beispiel: Im Array {52, 37, 63, 14, 17, 8, 6, 25} nehmen wir 25 als Drehpunkt. Nach dem ersten Durchgang wird die Liste folgendermaßen geändert.

{6 8 17 14 25 63 37 52}

Daher wird nach dem ersten Durchgang der Drehpunkt an seiner Position gesetzt, wobei alle Elemente links kleiner und alle Elemente größer als rechts sind. Jetzt werden 6 8 17 14 und 63 37 52 als zwei separate Sunarrays betrachtet, und dieselbe rekursive Logik wird auf sie angewendet, und wir werden dies bis dahin tun Das gesamte Array wird sortiert.

Wie funktioniert die schnelle Sortierung?

Die folgenden Schritte sind mit dem schnellen Sortieralgorithmus verbunden:

1. Nach Auswahl eines Elements als Pivot, in unserem Fall der letzte Index des Arrays, teilen wir das Array zum ersten Mal.
2. Bei der schnellen Sortierung nennen wir diese Partitionierung. Es ist nicht einfach, das Array in zwei Subarrays aufzuteilen, aber im Falle einer Partitionierung sind die Array-Elemente so positioniert, dass sich alle Elemente, die kleiner als der Pivot sind, auf der linken Seite des Pivots befinden und alle Elemente, die größer als der Pivot sind auf der rechten Seite sein.
3. Und das Pivot-Element befindet sich an seiner endgültigen sortierten Position.
4. Die Elemente links und rechts können möglicherweise nicht sortiert werden.
5. Dann wählen wir Subarrays, Elemente links vom Pivot und Elemente rechts vom Pivot aus und partitionieren sie, indem wir einen Pivot in den Subarrays auswählen.

Betrachten wir ein Array mit den Werten {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Nachfolgend haben wir Eine bildliche Darstellung, wie schnell das angegebene Array sortiert wird.

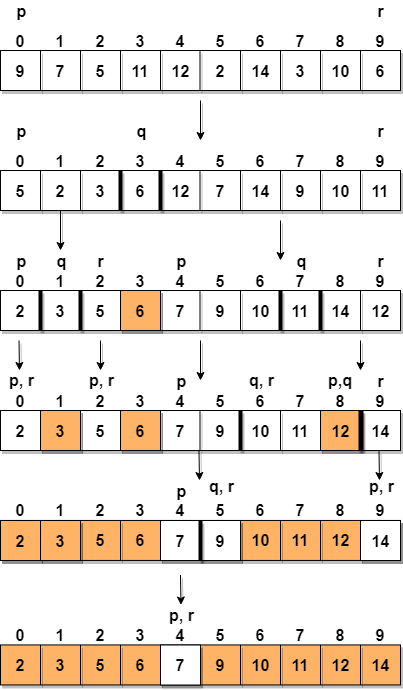
In Schritt 1 wählen wir das letzte Element als das aus Pivot, in diesem Fall 6, und rufen Sie partitioning auf, und ordnen Sie es daher neu an g das Array so, dass 6 an seiner endgültigen Position platziert wird und links alle Elemente kleiner als es sind und rechts davon alle Elemente größer als es.

Dann wählen wir das Subarray links und das Subarray rechts aus und wählen einen Drehpunkt für sie aus. Im obigen Diagramm haben wir 3 als Drehpunkt für das linke Subarray und 11 als Drehpunkt für das rechte Subarray.

Und wir fordern erneut partitioning.

Implementieren des Schnellsortierungsalgorithmus

Nachfolgend finden Sie ein einfaches C-Programm, das den Schnellsortierungsalgorithmus implementiert:

Komplexitätsanalyse der schnellen Sortierung

Für ein Array, bei dem die Partitionierung zu unausgeglichenen Subarrays führt, in einem Ausmaß, in dem auf der linken Seite keine Elemente mit allen Elementen vorhanden sind größer als der Drehpunkt, also auf der rechten Seite.

Und wenn Sie weiterhin unausgeglichene Subarrays erhalten, dann der Lauf Die ning-Zeit ist der schlechteste Fall, nämlich O(n2)

Wenn die Partitionierung zu nahezu gleichen Subarrays führt, ist die Laufzeit die beste mit einer zeitlichen Komplexität von O (n * log n).

Komplexität der Zeit im ungünstigsten Fall: O (n2)

Komplexität der Zeit im besten Fall: O (n * log n)

Durchschnittliche Zeitkomplexität: O (n * log n)

Raumkomplexität: O (n * log n)

Wie wir jetzt wissen, wird die Partitionierung von Subarrays nach der Partitionierung erzeugt unausgeglichen sind, dauert das schnelle Sortieren länger. Wenn jemand weiß, dass Sie den letzten Index ständig als Pivot auswählen, kann er Ihnen absichtlich ein Array zur Verfügung stellen, das im schlimmsten Fall zu einer schnellen Sortierung führt.

Um dies zu vermeiden, können Sie zufällig auswählen Schwenkelement auch. Es macht keinen Unterschied im Algorithmus, da Sie lediglich ein zufälliges Element aus dem Array auswählen, es mit dem Element am letzten Index austauschen, es zum Drehpunkt machen und mit der schnellen Sortierung fortfahren müssen. P. >

• Der für die schnelle Sortierung erforderliche Speicherplatz ist sehr gering, nur O(n*log n) zusätzlicher Speicherplatz ist erforderlich.
• Die schnelle Sortierung ist keine stabile Sortiertechnik, daher kann sich das Auftreten von zwei ähnlichen Elementen in der Liste während der Sortierung ändern.

Nachdem wir die schnelle Sortierung gelernt haben Algorithmus können Sie auch diese Sortieralgorithmen und ihre Anwendungen überprüfen:

• Einfügesortierung
• Auswahlsortierung
• Blasensortierung
• Sortierung zusammenführen
• Heap-Sortierung
• Zählsortierung