Algoritm de sortare rapidă

Sortare rapidă este una dintre diferitele tehnici de sortare care se bazează pe conceptul de divizare și cucerire, la fel ca fuzionează sort. Dar, în sortare rapidă, toate operațiunile de ridicare grele (lucrări majore) se fac în timp ce împărțim matricea în subarrays, în timp ce în cazul sortării merge, toate lucrările reale se întâmplă în timpul fuzionării subarrays-urilor. În caz de sortare rapidă, etapa de combinare nu face absolut nimic.

Se mai numește sortare de schimb de partiție. Acest algoritm împarte lista în trei părți principale:

1. Elemente mai mici decât elementul pivot
2. Element pivot (element central)
3. Elemente mai mari decât element pivot

Element pivot poate fi orice element din matrice, poate fi primul element, ultimul element sau orice element aleatoriu. În acest tutorial, vom lua elementul din dreapta sau ultimul element ca pivot.

De exemplu: În tabloul {52, 37, 63, 14, 17, 8, 6, 25}, luăm 25 ca pivot. Deci, după prima trecere, lista va fi modificată astfel.

{6 8 17 14 25 63 37 52}

Prin urmare, după prima trecere, pivotul va fi setat în poziția sa, cu toate elementele mai mici la stânga și toate elementele mai mari decât la dreapta. Acum, 6 8 17 14 și 63 37 52 sunt considerați ca două sunarrays separate și se va aplica aceeași logică recursivă și vom continua să facem acest lucru până matricea completă este sortată.

Cum funcționează sortarea rapidă?

Urmează pașii implicați în algoritmul de sortare rapidă:

1. După selectarea unui element ca pivot, care este ultimul index al tabloului în cazul nostru, împărțim tabloul pentru prima dată.
2. În sortare rapidă, numim această partiționare. Nu este simplă descompunerea matricei în 2 subarraiuri, dar în cazul partiționării, elementele matricei sunt așa poziționate încât toate elementele mai mici decât pivotul vor fi pe partea stângă a pivotului și toate elementele mai mari decât pivotul vor fi să fie în partea dreaptă a acestuia.
3. Iar elementul pivot va fi la poziția sa finală de sortare.
4. Este posibil ca elementele din stânga și dreapta să nu fie sortate.
5. Apoi alegem subarrays, elemente din stânga pivotului și elemente din dreapta pivotului și efectuăm partiționarea pe ele alegând un pivot în subarrays.

Să considerăm o matrice cu valori {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Mai jos, avem o reprezentare picturală a cât de rapidă va sorta matricea dată.

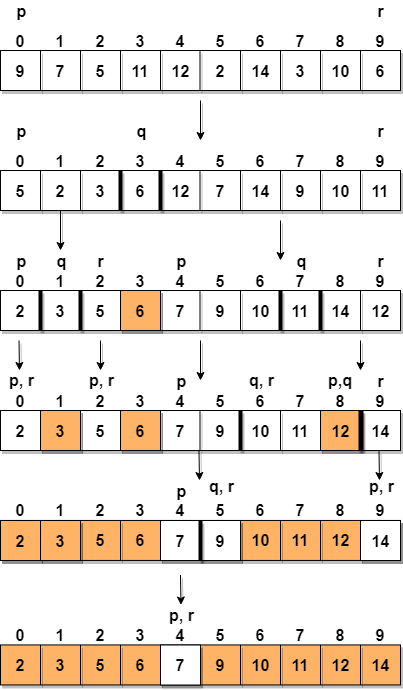
În pasul 1, selectăm ultimul element ca pivot, care este 6 în acest caz și apelați la partitioning, prin urmare, rearanjați g matricea în așa fel încât 6 va fi plasat în poziția sa finală și la stânga sa vor fi toate elementele mai mici decât ea și la dreapta sa, vom avea toate elementele mai mare decât ea.

Apoi alegem subarray-ul din stânga și subarray-ul din dreapta și selectăm un pivot pentru ele, în diagrama de mai sus, am ales 3 ca pivot pentru subarray-ul stâng și 11 ca pivot pentru subarray-ul din dreapta.

Și apelăm din nou la partitioning.

Implementarea algoritmului de sortare rapidă

Mai jos avem un program simplu C care implementează algoritmul de sortare rapidă:

Analiza complexității sortării rapide

Pentru o matrice, în care partiționarea duce la subarraiuri dezechilibrate, într-o măsură în care în partea stângă nu există elemente, cu toate elementele mai mare decât pivotul, deci pe partea dreaptă.

Și dacă continuați să obțineți subarraiuri dezechilibrate, atunci rulați timpul este cel mai rău caz, care este O(n2)

În cazul în care partiționarea duce la submatricii aproape egale, atunci timpul de rulare este cel mai bun, cu complexitatea timpului ca O (n * log n).

Cel mai rău caz de complexitate în timp: O (n2)

Cel mai bun caz de complexitate în timp: O (n * log n)

Complexitate medie în timp: O (n * log n)

Complexitate spațială: O (n * log n)

După cum știm acum, dacă partiționarea subarraysului este produsă după partiționare sunt dezechilibrate, sortarea rapidă va dura mai mult timp pentru a termina. Dacă cineva știe că alegeți ultimul index ca pivot tot timpul, vă poate furniza în mod intenționat o matrice care va duce la cel mai rău caz de rulare pentru o sortare rapidă.

Pentru a evita acest lucru, puteți alege aleatoriu element pivot prea. Nu va face nicio diferență în algoritm, deoarece tot ce trebuie să faceți este să alegeți un element aleatoriu din matrice, să îl schimbați cu elementul la ultimul index, să îl faceți pivot și să continuați cu sortarea rapidă.

• Spațiul necesar pentru sortarea rapidă este foarte redus, este necesar doar O(n*log n) spațiu suplimentar.
• Sortarea rapidă nu este o tehnică stabilă de sortare, deci ar putea schimba apariția a două elemente similare din listă în timpul sortării.

Acum că am învățat sortarea rapidă algoritm, puteți verifica și acești algoritmi de sortare și aplicațiile acestora:

• Sortare prin inserție
• Sortare prin selecție
• Sortare prin bule
• Merge sort
• Sortare heap
• Sortare numărare