Algorytm szybkiego sortowania

Szybkie sortowanie to jedna z różnych technik sortowania, która opiera się na koncepcji dziel i rządź, podobnie jak scal sortowanie. Ale w szybkim sortowaniu cała ciężka praca (główna praca) jest wykonywana podczas dzielenia tablicy na podtablice, podczas gdy w przypadku sortowania przez scalanie cała prawdziwa praca odbywa się podczas łączenia podtablic. W przypadku szybkiego sortowania, etap łączenia nie robi absolutnie nic.

Nazywa się go również sortowaniem z wymianą partycji. Algorytm dzieli listę na trzy główne części:

1. Elementy mniejsze niż element Pivot
2. Element Pivot (element centralny)
3. Elementy większe niż element pivot

Element Pivot może być dowolnym elementem tablicy, może to być pierwszy element, ostatni element lub dowolny element losowy. W tym samouczku jako wartość przestawną weźmiemy skrajny prawy element lub ostatni element.

Na przykład: w tablicy {52, 37, 63, 14, 17, 8, 6, 25} bierzemy 25 jako pivot. Dlatego po pierwszym przebiegu lista zostanie zmieniona w ten sposób.

{6 8 17 14 25 63 37 52}

Zatem po pierwszym przejściu pivot zostanie ustawiony na swoim miejscu, z wszystkimi elementami mniejszymi od niego po jego lewej stronie i wszystkimi elementami większymi niż po jego prawej stronie. Teraz 6 8 17 14 i 63 37 52 są uważane za dwie oddzielne tablice słoneczne i zostanie do nich zastosowana ta sama rekurencyjna logika i będziemy to robić do cała tablica jest sortowana.

Jak działa szybkie sortowanie?

Poniżej przedstawiono kroki niezbędne do wykonania algorytmu szybkiego sortowania:

1. Po wybraniu elementu jako pivot, który jest ostatnim indeksem tablicy w naszym przypadku, dzielimy tablicę po raz pierwszy.
2. W szybkim sortowaniu nazywamy to partycjonowaniem. Nie jest to proste rozbicie tablicy na 2 podtablice, ale w przypadku podziału elementy tablicy są tak ustawione, że wszystkie elementy mniejsze niż oś obrotu będą znajdować się po lewej stronie osi, a wszystkie elementy większe niż oś obrotu będą znajdować się po jego prawej stronie.
3. A element pivot będzie w ostatecznej posortowanej pozycji.
4. Elementy po lewej i prawej stronie nie mogą być sortowane.
5. Następnie wybieramy podtablice, elementy po lewej stronie pivota i elementy po prawej stronie pivot i wykonujemy na nich partycjonowanie, wybierając punkt obrotu w podtablicach.

Rozważmy tablicę z wartościami {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Poniżej mamy obrazkowa reprezentacja tego, jak szybkie sortowanie posortuje daną tablicę.

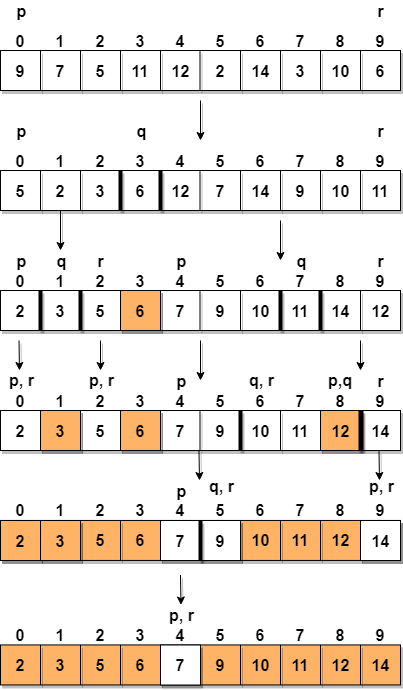
W kroku 1 wybieramy ostatni element jako pivot, czyli w tym przypadku 6, i wywołanie partitioning, więc ponownie uporządkuj g tablica w taki sposób, że 6 zostanie umieszczona w jej ostatecznej pozycji, a po jej lewej stronie będą wszystkie elementy mniejsze od niej, a po jej prawej będziemy mieli wszystkie elementy większe niż to.

Następnie wybieramy podtablicę po lewej i podtablicę po prawej i wybieramy dla nich oś obrotu. Na powyższym schemacie wybraliśmy 3 jako punkt obrotu dla lewej podtablicy i 11 jako punkt obrotu dla prawej podtablicy.

I ponownie wzywamy partitioning.

Implementacja algorytmu szybkiego sortowania

Poniżej mamy prosty program w C implementujący algorytm szybkiego sortowania:

Analiza złożoności szybkiego sortowania

Dla tablicy, w której partycjonowanie prowadzi do niezrównoważonych podtablic, do tego stopnia, że po lewej stronie nie ma żadnych elementów, ze wszystkimi elementami większa niż pivot, a więc po prawej stronie.

A jeśli nadal uzyskujesz niezrównoważone podtablice, to bieg Czas ning jest najgorszym przypadkiem, czyli O(n2)

W przypadku gdy podział prowadzi do prawie równych podtablic, wtedy czas działania jest najlepszy, przy złożoności czasowej O (n * log n).

Złożoność czasowa najgorszego przypadku: O (n2)

Złożoność czasowa najlepszego przypadku: O (n * log n)

Średnia złożoność czasowa: O (n * log n)

Złożoność przestrzeni: O (n * log n)

Jak wiemy teraz, jeśli podtablice partycjonują po partycjonowaniu są niezrównoważone, szybkie sortowanie zajmie więcej czasu. Jeśli ktoś wie, że cały czas wybierasz ostatni indeks jako przestawny, może celowo dostarczyć Ci tablicę, co spowoduje najgorszy czas działania dla szybkiego sortowania.

Aby tego uniknąć, możesz wybrać losowo element obrotowy też. Nie zrobi to żadnej różnicy w algorytmie, ponieważ wszystko, co musisz zrobić, to wybrać losowy element z tablicy, zamienić go na element o ostatnim indeksie, ustawić go w osi obrotu i kontynuować szybkie sortowanie.

• Miejsce wymagane do szybkiego sortowania jest bardzo mniejsze, wymagana jest tylko O(n*log n) dodatkowa przestrzeń.
• Szybkie sortowanie nie jest stabilną techniką sortowania, więc może zmienić występowanie dwóch podobnych elementów na liście podczas sortowania.

Teraz, gdy nauczyliśmy się szybkiego sortowania algorytm, możesz sprawdzić te algorytmy sortowania i ich zastosowania:

• Sortowanie przez wstawianie
• Sortowanie przez wybór
• Sortowanie w dymku
• Sortowanie przez scalanie
• Sortowanie na stosie
• Sortowanie według liczenia