Quick Sort Algorithm

Quick Sort is een van de verschillende sorteertechnieken die is gebaseerd op het concept van Divide and Conquer, net als samenvoegen sorteren. Maar bij snel sorteren wordt al het zware werk (groot werk) gedaan terwijl de array in subarrays wordt verdeeld, terwijl in het geval van samenvoegen sorteren, al het echte werk gebeurt tijdens het samenvoegen van de subarrays. In het geval van snel sorteren, doet de combinatiestap helemaal niets.

Het wordt ook partitie-uitwisselingssortering genoemd. Dit algoritme verdeelt de lijst in drie hoofddelen:

1. Elementen kleiner dan het Pivot-element
2. Pivot-element (centraal element)
3. Elementen groter dan het pivot-element

Pivot-element kan elk element uit de array zijn, het kan het eerste element, het laatste element of een willekeurig element zijn. In deze tutorial nemen we het meest rechtse element of het laatste element als spil.

Bijvoorbeeld: in de array {52, 37, 63, 14, 17, 8, 6, 25} nemen we 25 als draaipunt. Dus na de eerste bewerking wordt de lijst als volgt gewijzigd.

{6 8 17 14 25 63 37 52}

Na de eerste doorgang zal de pivot dus op zijn positie worden gezet, met alle elementen kleiner aan de linkerkant en alle elementen groter dan aan de rechterkant. Nu worden 6 8 17 14 en 63 37 52 beschouwd als twee afzonderlijke sunarrays, en dezelfde recursieve logica zal erop worden toegepast, en we zullen dit blijven doen totdat de volledige array is gesorteerd.

Hoe werkt snel sorteren?

Hieronder volgen de stappen die betrokken zijn bij het algoritme voor snel sorteren:

1. Na het selecteren van een element als pivot, wat in ons geval de laatste index van de array is, verdelen we de array voor de eerste keer.
2. Bij snel sorteren noemen we dit partitionering. Het is niet eenvoudig om de array in 2 subarrays op te splitsen, maar in het geval van partitionering zijn de array-elementen zo gepositioneerd dat alle elementen kleiner dan het draaipunt zich aan de linkerkant van het draaipunt bevinden en alle elementen groter dan het draaipunt. aan de rechterkant ervan staan.
3. En het pivot-element bevindt zich op de uiteindelijke gesorteerde positie.
4. De elementen aan de linker- en rechterkant mogen niet worden gesorteerd.
5. Vervolgens kiezen we submatrices, elementen aan de linkerkant van het draaipunt en elementen aan de rechterkant van het draaipunt, en we voeren partitionering uit door een draaipunt in de submatrices te kiezen.

Laten we eens kijken naar een array met waarden {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Hieronder hebben we een grafische weergave van hoe snel sorteren de gegeven array zal sorteren.

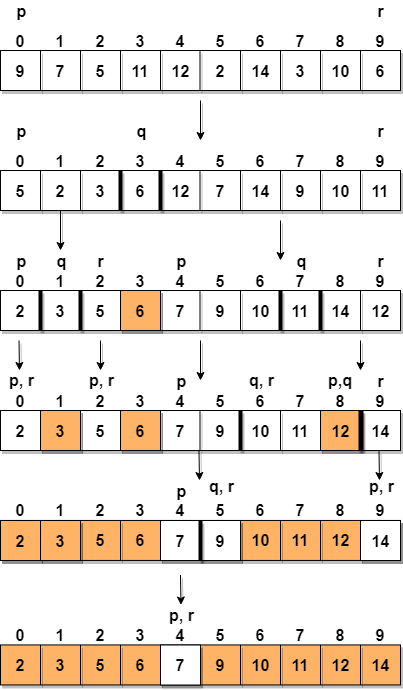
In stap 1 selecteren we het laatste element als de pivot, wat in dit geval 6 is, en roep partitioning aan, dus herschik g de array op een zodanige manier dat 6 op zijn uiteindelijke positie wordt geplaatst en links daarvan alle elementen minder dan de array en rechts daarvan hebben we alle elementen groter dan het.

Vervolgens kiezen we de submatrix aan de linkerkant en de submatrix rechts en selecteren we een draaipunt voor hen, in het bovenstaande diagram hebben we gekozen voor 3 als draaipunt voor de linker submatrix en 11 als draaipunt voor de rechter submatrix.

En we roepen opnieuw partitioning.

Implementatie van Quick Sort-algoritme

Hieronder hebben we een eenvoudig C-programma dat het Quick sort-algoritme implementeert:

Complexiteitsanalyse van Quick Sort

Voor een array, waarin partitionering leidt tot ongebalanceerde subarrays, in een mate waarin er aan de linkerkant geen elementen zijn, met alle elementen groter dan het draaipunt, dus aan de rechterkant.

En als steeds ongebalanceerde subarrays worden, dan is de run ning-tijd is het ergste geval, dat is O(n2)

Waar alsof partitionering leidt tot bijna gelijke subarrays, dan is de looptijd de beste, met tijdcomplexiteit als O (n * log n).

Worst Case Time Complexity: O (n2)

Best Case Time Complexity: O (n * log n)

Gemiddelde tijdcomplexiteit: O (n * log n)

Ruimtecomplexiteit: O (n * log n)

Zoals we nu weten, dat als subarrays worden gepartitioneerd na partitionering zijn onevenwichtig, zal snel sorteren meer tijd kosten om te voltooien. Als iemand weet dat je de laatste index de hele tijd als pivot kiest, kunnen ze je opzettelijk een array geven, wat zal resulteren in looptijd in het ergste geval voor snel sorteren.

Om dit te voorkomen, kun je willekeurig kiezen draai-element ook. Het maakt geen enkel verschil in het algoritme, het enige wat je hoeft te doen is een willekeurig element uit de array kiezen, het verwisselen met het element bij de laatste index, het de spil maken en doorgaan met snel sorteren.

• De ruimte die nodig is voor snel sorteren is veel minder, alleen O(n*log n) extra ruimte is vereist.
• Snel sorteren is geen stabiele sorteertechniek, dus het kan het voorkomen van twee vergelijkbare elementen in de lijst tijdens het sorteren veranderen.

Nu we Snel sorteren hebben geleerd algoritme, kunt u deze sorteeralgoritmen en hun toepassingen ook bekijken:

• Invoegsortering
• Selectie-sortering
• Bubbelsortering
• Sorteren samenvoegen
• Sorteren op heap
• Sorteren en sorteren