Poisson-distribusjon
Gitt en Poisson-prosess, er sannsynligheten for å oppnå nøyaktig 
suksesser i 
forsøk gitt av grensen for en binomial fordeling
 |
(1)
|
Ser på fordelingen som en funksjon av forventet antall suksesser
 |
(2)
|
i stedet for prøvestørrelsen 
for fast 
blir ligning (2) da
 |
(3)
|
La prøvestørrelsen 
bli stor, og fordelingen nærmer seg da
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
som er kjent som Poisson-distribusjonen (Papoulis 1984, s. 101 og 554; Pfeiffer og Schum 1973, s. 200). Merk at prøvestørrelsen 
har falt helt ut av sannsynlighetsfunksjonen, som har samme funksjonelle form for alle verdiene av 
.
Poisson-distribusjonen er implementert i WolframLanguage som PoissonDistribution.
Som forventet normaliseres Poisson-fordelingen slik at sannsynligheten er lik 1, siden
 |
(9 )
|
Forholdet mellom sannsynligheter er gitt av
 |
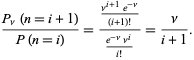(10)
|
Poisson-fordelingen når et maksimum når
 |
(11)
|
der er Euler-Mascheroni-konstanten og 
er et harmonisk tall, som fører til den transcendentale ligningen
 |
(12)
|
som ikke kan løses nøyaktig for 
.
Den øyeblikksgenererende funksjonen til Poisson-fordelingen er gitt av
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
så
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, s. 554).
De rå øyeblikkene kan også beregnes direkte ved summering, noe som gir en uventet forbindelse med Bell-polynomet 
og Stirling-tall av den andre typen,
 |
(21)
|
kjent som Dobińskis formel.Derfor
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
De sentrale momentene kan deretter beregnes som
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
så gjennomsnittet, variansen, skjevheten og kurtosisoverskuddet er
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
Den karakteristiske funksjonen for Poissondistribusjon er
(Papoulis 1984, s. 154 og 554), og den kumulantgenererende funksjonen er
 |
(34)
|
så
 |
(35)
|
Gjennomsnittlig avvik for Poisson-fordelingen gitt av
 |
(36)
|
Poisson-fordelingen kan også uttrykkes som
 |
(37)
|
 |
(38)
|
Den momentgenererende funksjonen til aPoisson-fordeling i to variabler er gitt av
 |
(39)
|
Hvis de uavhengige variablene 
, 
, …, 
har Poisson-distribusjoner med parametere 
, 
, …, 
, deretter
 |
(40)
|
har en Poisson-fordeling med parameter
 |
(41)
|
Dette kan sees siden kumulantgenereringsfunksjonen er
 |
(42)
|
 |
(43)
|
En generalisering av Poisson-distribusjonen har blitt brukt av Saslaw (1989) for å modellere den observerte klyngen av galakser i universet. Formen på denne fordelingen er gitt av
 |
(44)
|
hvor 
er antall galakser i et volum 
, 
, 
er den gjennomsnittlige tettheten til galakser, og 
, med 
er forholdet mellom gravitasjonsenergi og kinetikken energi av særegne bevegelser, la 
gir
 |
(45)
|
som faktisk er en Poisson-fordeling med 
. På samme måte gir 
.