Måling: Oppdage formler for område

Arealformler

Studenter som har den uformelle forestillingen om at området er «mengden 2-D «ting» «inneholdt i en region kan finne på seg selv de fleste formlene som de ofte bare blir bedt om å huske. Hver formel de gjenoppfinner, bidrar til å styrke forståelsen (og hukommelsen) for de andre formlene de kjenner. (Se også overflateareal.)

Areal av rektangler

Ved å velge et kvadrat som arealeenheten får vi en intuitiv ide om arealet av rektangler. Hvis vi bestemmer oss for at arealet til dette kvadratet er 1, vil et rektangel som er 7 ganger så langt ha 7 × 1 som sitt område.

Et rektangel som er dobbelt så høyt som vil ha dobbelt så stort areal, så området til er 2 × 7 enheter. Vi kan telle de to radene på syv firkanter. Tilsvarende har 3 rader med 7 firkanter (eller 7 kolonner med 3 firkanter), totalt 7 × 3 firkanter, så arealet er 21 kvadrat enheter.

Antall firkanter i en rad er lengden på rektangelet. Antall rader er høyden på rektangelet. Så området er lengde × høyde.

Fordi et rektangel kan tegnes i en skråstilling, er «høyde» definert til å bety «retningen vinkelrett på basen,» og «base» er definert til å være, vel, uansett hvilken side du velger å være.

Det fungerer for å telle tall. Det fungerer til og med for brøker. 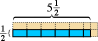Det blå rektangelet som vises her, måler halvparten lengdeenhet høy med fem og halv lengdeenheter bred. Hvis vi velger tilsvarende kvadrat som vår arealenhet, ser vi at det blå rektangelet inneholder fem halve enheter areal og en kvart enhet areal, eller et totalt to og tre fjerdedelenheter. (De rosa delene viser fullføringen av hver firkantede arealenhet.)

For å inkludere alle tall, definerer vi arealet til et rektangel som skal være base × høyde (hvor «base» og «høyde» betyr lengden på disse sidene, målt i de samme enhetene).

Areal av parallellogrammer

Få ideen

Vi kan finne ut en formel for arealet til et parallellogram ved å dissekere ing parallellogrammet og omorganisere delene for å lage et rektangel. Fordi parallellogrammet og rektangelet er sammensatt av de samme delene, har de nødvendigvis samme område. (Se definisjonen av område for mer om hvorfor disse områdene er de samme.)

Vi kan se at de også har nøyaktig samme bunnlengde (blå) og nøyaktig samme høyde (grønn). Fordi base × høyde gir arealet til rektangelet, kan vi bruke de samme målene på parallellogrammet for å beregne arealet: base × høyde. (Som før måles «høyde» vinkelrett på underlaget, og «underlag» er hvilken side du valgte først. Se parallellogram.)

Kuttet vist ovenfor gjør det enkelt å se at bunnlengden er uendret. Den vinkelrette kuttingen kan faktisk gjøres hvor som helst langs basen.

Avskjæring av hullene

Intuisjon og bevis

Denne disseksjonen gir en intuitiv forståelse av områdeformelen for et parallellogram, en grunn til at det skal være hva det er. Men vi har ikke stilt spørsmålstegn ved om disseksjonen virkelig «fungerer.» Når vi kutter parallellogrammet og omorganiserer delene, forventer vi å få og resultatet ser absolutt slik ut. utseende kan være villedende. Hva forsikrer oss om at når vi flytter den trekanten, er resultatet et rektangel? Hva om det er mer som (skjønt mindre overdrevet)? Hvis resultatet ikke er alltid et perfekt rektangel, kan vi ikke bruke vår kunnskap om rektangelets arealformel til å utvikle en formel for parallellogrammet. På videregående skole vil studentene kunne bevise at de to delene av parallellogrammet, når de er satt sammen riktig, lager et rektangel I klassene K-8 må studentene for det meste stole på det visuelle eksperimentet og få en intuitiv følelse. Lær mer om hvorfor disse disseksjonene fungerer.

Hva om vi velger kortsiden for å være basen?

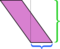
Vi står fritt til å velge hvilken som helst side som base; «høyde» er definert å være målt vinkelrett på den siden vi velger som base. Hvis vi tar kortsiden (blå) som basen, er ikke disseksjonen vist ovenfor like overbevisende. Å kutte langs den høyden og omorganisere delene etterlater et rot:

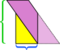
I dette spesielle eksemplet, vi kan redde rotet ved å lage en kutt til, 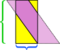men hva om parallellogrammet var enda lengre og tynnere?

Det viser seg at ethvert parallellogram, uansett hvor lang og tynn, kan dissekeres på denne måten slik at delene – kanskje mange av dem – kan omorganiseres til et rektangel. Men det kreves mer arbeid for å vise at dette alltid kan gjøres. Vi trenger en annen idé.

En litt annen disseksjonside gjør livet mye lettere i dette tilfellet. (På egen hånd kan du vise at det også fungerer i den originale saken.)

• Legg parallellogrammet i et rektangel.
• De to delene av rektangelet som ikke er inne i parallellogrammet, er kongruente trekanter.
• Skyv en av disse trekantene mot den andre til de møtes for å danne et rektangel. 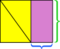Fordi det totale arealet til det ytre rektangelet ikke har endret seg (det er det samme rektangelet som før) og det gule området ikke har endret seg (brikkene nettopp flyttet rundt), er forskjellen mellom dem – de lilla områdene – må være de samme. Som før kan vi også se at dimensjonene til det rektangulære lilla området er basen og høyden på det opprinnelige parallellogrammet.

Intuisjon og bevis, reprise : Igjen gir disseksjonen den essensielle innsikten, men det tar litt mer arbeid å sikre at de to gule trekantene, som absolutt ser ut som om de passer sammen for å lage et rektangel, virkelig passer nøyaktig, og ikke bare nesten. p>

Hvorfor er det viktig å være så forsiktig?

Når vi bygger andre områdeformler (nedenfor), vil vi bruke hvordan vi finner arealet til et parallellogram, og så ønsker vi å kunne stole på regelen vi har funnet. Vi kan være sikre på at omorganisering av deler ikke endrer området: det er tross alt hvordan vi definerer område. Men vi må også være sikre på at delene passer sammen slik vi hevder at de gjør, ellers kan vi ikke stole på målingene vi har gjort. Og vi må være sikre på at basis × høyderegelen ikke avhenger av et heldig valg av base.

I de fleste læreplaner har ikke elevene en systematisk nok base av geometriske kunnskaper før 8. klasse til å lage lyd bevis på at disse disseksjonene fungerer. Men den intuitive forståelsen er nok til å forklare og rettferdiggjøre formlene, og en god forankring for senere geometriske studier.

Område med trekant

Å vite hvordan vi skal finne arealet til et parallellogram hjelper oss finne området til en trekant.

Dissekere trekanten

Vi kan dissekere trekanten i to deler – en av dem en trekant og en av dem en trapesformet – ved å skjære den parallelt til basen. Hvis vi kutter høyden nøyaktig i to med den delen, passer de to delene sammen for å lage et parallellogram med samme base, men halvparten av høyden.

Så base × halv høyde gir arealet av trekanten. En lignende disseksjon viser halv base × høyde. En av dem reduseres til bh.

Dobling av trekanten og deretter halvering av det resulterende området

En annen måte å tenke på: to kopier av trekanten lager et parallellogram med samme base og samme høyde som trekanten.

Parallellogrammets areal er base × høyde, men det er dobbelt så stort arealet av trekanten, så trekantsarealet er av base × høyde, slik vi så med disseksjonsmetoden.

(Som alltid , velg en «base» og måle høyden vinkelrett på den basen, fra basen til det motsatte toppunktet.)

Areal av trapesform

Dobling av trapesformet og deretter halvering av det resulterende området

Som det var sant med trekanten, kan to kopier av en trapesform passe sammen for å lage et parallellogram.

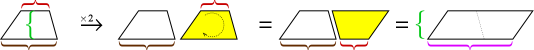
Høyden til parallellogrammet er den samme som trapesformens høyde, men basen er summen av trapesformens to baser. Parallellogrammets areal er altså høyden × (base1 + base2). Men det området er to trapeser, så vi må kutte det i halvparten for å få området til trapeset.

Disseksjon av trapesformet

Vi kunne også dissekere trapesformen slik vi dissekerte trekanten, med en enkelt skive som kutter høyden i to. De to delene passer sammen for å lage et parallellogram hvis base er summen av de to basene av trapesformet, men hvis høyde er halvparten av trapesformen.

Når det gjelder trapesformet, kan basene ikke velges etter ønske. De to parallelle sidene er basene, og høyden er som alltid den vinkelrette avstanden fra en base til det motsatte.

Arealet til dette parallellogrammet er høyden (halvhøyde av trapesformet) ganger basen (summen av trapesformen), så arealet er halvhøyde × (base1 + base2). Fordi parallellogrammet er laget av nøyaktig samme «ting» som trapesformet, er det også området til trapesformet.

Uansett er arealet til trapesformet × høyde × (base1 + base2).

Område for andre spesielle firkanter

Areal av rombe

Området for en rombe kan bli funnet ved å kutte og omorganisere bitene for å danne et parallellogram. Dette kan gjøres på flere måter:

1. Skjær over den kortere diagonalen (a) for å danne to kongruente trekanter. Flytt den nedre halvdelen av trekanten ved siden av den øvre halvdelen for å danne et parallellogram. Den kortere diagonalen (a) blir basen til parallellogrammet, og halvparten av den lengre diagonalen (b) blir høyden på parallellogrammet. Dermed er arealet av romben et * b eller produktet av diagonalene, som er standardformelen for romben.
2. En annen lignende måte er å kutte romben i fire kongruente trekanter og omorganisere dem til et rektangel med den kortere diagonalen som basen og halvparten den lengre diagonalen som høyden.
3. Etter kutting romben i to kongruente trekanter, kan vi beregne arealet til en av trekanten, som er * base (a) * høyde ( b) = ab. Multipliser deretter med to siden det er to av dem: 2 * ab = ab.

Drageområde

Området til en drage kan bli funnet som ligner området til en rombe. Å kutte over den lengre diagonalen gir to kongruente trekanter. Hvis vi omorganiserer dem, kan vi danne et parallellogram med den lengre diagonalen (b) som base og halvparten den kortere diagonalen (a) som høyden. Så blir området b * a = ab. En mer komplisert tilnærming innebærer litt algebra. Skjær dragen over den kortere diagonalen for å danne to trekanter med den kortere diagonalen (a) som underlag. Dermed er arealet til den første trekanten a * squiggly, hvor squiggly er høyden. Arealet til den andre trekanten er a * (b – squiggly), hvor (b – squiggly) er den gjenværende delen av den lengre diagonalen. Det totale arealet blir dermed ( a * squiggly) + ( a * (b – squiggly)). Faktorering av a, vi har a (squiggly + b – squiggly) = ab.

Vel, hva vet du. I utgangspunktet trenger du bare å kjenne formelen for området til et parallellogram og deretter utlede formelen for de andre.