Hvordan beregne volumet

Beregne volumet

Volumet måles i kuber (eller kubiske enheter).

Hvor mange kuber er det i dette rektangulære prismaet (kuboid)?

Vi kan telle kubene, selv om det er raskere å ta lengden, bredden og høyden og bruke multiplikasjon. Det rektangulære prismen ovenfor har et volum på 48 kubikk enheter.

Volumet til et rektangulært prisme er = lengde x bredde x høyde

Eksempler på beregning av arealet til et rektangel

Vi må gjøre to multiplikasjoner for å beregne volumet. Vi beregner arealet til det ene ansiktet (eller siden) og multipliserer det med høyden. Eksemplene nedenfor viser hvordan det er tre måter å gjøre dette på.

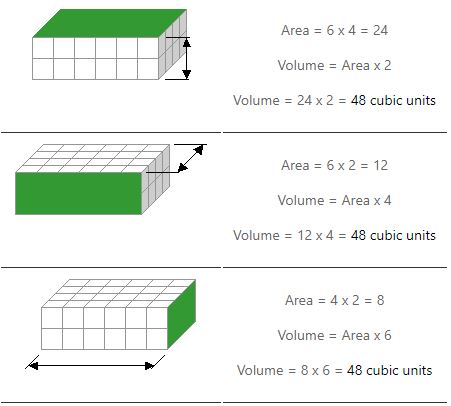
Legg merke til hvordan vi får det samme svaret uansett hvilken side vi bruker for å finne et område.

Når barnet ditt begynner å jobbe med areal og omkrets, vil han eller hun vanligvis jobbe med to dimensjoner – firkanter, rektangler, trekanter osv. som vises på papir som flate – det er ingen dybde eller 3. dimensjon. Arbeid med volum involverer tre dimensjoner. Forsikre deg om at barnet ditt er klar over dette og ikke tenker på kubene og andre 3D-figurer som vises på papir som bare en annen «form på siden.» Vis dem virkelige bokser, og vis hvordan disse kan tegnes (eller representeres) på et todimensjonalt stykke papir. Med andre ord, sørg for at sammenhengen mellom hva som står på papiret og hva det representerer i den virkelige verden er laget. .

Enheter for å måle volum

Det er veldig store forskjeller mellom måleenheter for volum. For eksempel er det 100 centimeter på 1 meter, men det er 1.000.000 (ja, 1 million ) kubikkcentimeter i en kubikkmeter.

Hvorfor den store forskjellen? Fordi i volum har vi ikke bare lengde; vi har lengde, bredde og høyde. Eksemplet på sukkerterningen nedenfor viser dette.

Hvor mye sukker? 1 m3 eller 1.000.000 cm3

Tenk å fylle en veldig stor boks (den vil være 1 meter bred, 1 meter, lang og en meter høy) med sukkerbiter (med hver side 1 centimeter).

	Trinn 1: en rad langs bunnen av boksen – det ville være 100 sukkerbiter
	Trinn 2: dekk resten av bunnen av esken – som vil gi totalt 100 rader hver med 100 sukkerbiter. 100 x 100 = 10.000 sukker og terninger i bunnen av den store esken.
	Trinn 3: Gjenta dette 99 ganger til det er lag med 10.000 kuber stablet 100 dype. 10.000 x 100 = 1.000.000 sukkerbiter

Det er 1 000 000 cm3 i 1 m3 – vær forsiktig så du ikke har for mye sukker!

Det er andre enheter for å måle volum; kubikkmeter, kubikkmeter, kubikkmeter er alle enheter som brukes til å måle volum. Milliliter, liter, gallon brukes også spesielt når du måler væsker.

Ikke glem wee 3

Vi skriver kubikkstørrelser ved hjelp av en liten 3 ved siden av enheten.
Vi skriver mm3, cm3, m3, km3, cm3
Vi kan si «85 centimeter kubikk» eller «85 kubikkcentimeter»

Eksempler på beregning av volum av rektangulære prismer

	Volum = Lengde x Bredde x Høyde Volum = 12 cm x 8 cm x 6 cm = 576 cm3
	Volum = Lengde x Bredde x Høyde Volum = 20 mx 2 mx 2 m = 80 m3
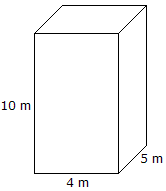	Volum = Lengde x Bredde x Høyde volum = 10 mx 4 mx 5 m = 200 m3

Volum av en sylinder

Beregning av volumet til en sylinder der innebærer å multiplisere basisområdet med sylinderens høyde. Basen til en sylinder er sirkulær og formelen for sirkelarealet er: areal av en sirkel = πr2. Det er mer her på området for en sirkel.

Volum = Baseareal x Høyde Volum = πr2 xh Volum = πr2 h

Merk: i eksemplene nedenfor vi vil bruke 3.14 som en omtrentlig verdi for π (Pi).

Eksempel på beregning av volumet til en sylinder

Målene er i cm.

Volum = πr2 h Volum = 3.14 x 3 x 3 x 8 Volum = 226,08 cm3

Volum av en kjegle

Volumet av en kjegle er lik en tredjedel volumet av en sylinder med samsvarende høyde og areal av bunnen. Dette gir formelen for volumet av en kjegle som vist nedenfor.

Volum = 1/3 πr2h

Eksempel på beregning av volumet på en kjegle

Dimensjoner er i cm.

Volum = 1/3 πr2 h Volum = 1/3 x 3,14 x 2 x 2 x 7 Volum = 29,31 cm3

Volum av en sfære

Formelen for volumet til en sfære er vist nedenfor.

Volum = 4/3 πr3

Eksempel på beregning av volumet til en sfære

Dimensjonene er i cm.

Volum = 4/3 πr3 Volum = 4/3 x 3,14 x 4 x 4 x 4 Volum = 267,95 cm3

Utskriftsvennlige volumark

Bruk regnearket nedenfor til å øve på å beregne volumer.

• Finne volum i kubiske enheter – rektangulære prismer og kompositter
• Volum av rektangulære prismer
• Volum av rektangulære prismer
• Volum av «virkelige» objekter, f.eks. av kornboks
• Beregning av volumer f.eks. av trekantede prismer og sylindere

Du får andre regneark for geometri på omkrets, areal og mer her.