Hvordan beregne areal
Beregne areal
Areal måles i kvadrater (eller kvadratiske enheter).
Hvor mange kvadrater er i dette rektangelet? / p>

Vi kan telle rutene ellers kan vi ta lengden og bredden og bruk multiplikasjon. Rektangelet over har et areal på 15 kvadrat enheter.
Arealet til et rektangel er = lengde x bredde
Eksempler på beregning av arealet til et rektangel
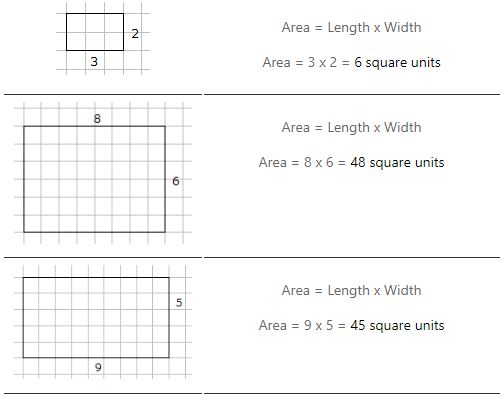
Enheter for å måle areal
Vi måler areal ved hjelp av firkanter. Vi bruker forskjellige størrelser på kvadrater, avhengig av hvor stort eller lite et område er.
| Eksempel | Lengden på siden på firkanter | Enhet |
| Størrelsen på spik på tommelen | Millimeter | mm2 |
| Papirstørrelse | Centimeter | cm2 |
| Størrelse på et rom | Meter | m2 |
| Byens størrelse | Kilometer | km2 |
Ikke glem wee 2
Vi skriver firkantede størrelser ved hjelp av en liten 2 ved siden av enheten.
Vi skriver mm2, cm2, m2, km2, cm2
Vi kan si «63 millimeter kvadrat» eller «63 kvadrat millimeter»
Vi kunne bruke små firkanter for å måle store områder. Det eneste problemet med dette er at vi ender med å bruke veldig store tall. For eksempel kan et felt måles til 5.000.000.000 kvadratmillimeter når 5.000 kvadratmeter ville være en mye lettere størrelse å si, skrive og visualisere.
Du vil sannsynligvis høre flere enheter for å måle areal; kvadratmeter, kvadratmeter, kvadratmeter, kvadratkilometer, dekar, hektar er alle enheter som brukes til å måle areal.
Flere eksempler på beregning av areal
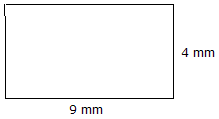 |
Areal = Lengde x Bredde Areal = 9 mm x 4 mm = 36 mm2 |
 |
Areal = Lengde x Bredde Areal = 7 cm x 6 cm = 42 cm2 |
 |
Areal = Lengde x Bredde Areal = 8 mx 2 m = 16 m2 |
 |
Areal = Lengde x Bredde Areal = 7 km x 5 km = 35 km2 |
Område av en firkant
Lengden og bredden på et kvadrat er den samme, så vi trenger bare å multiplisere lengden med lengden.
| Areal = Lengde x Lengde Areal = 6 cm x 6 cm = 36 cm2 |
Område av en sirkel
Området til en sirkel = πr2
hvor r er radiusen til sirkelen og π er forholdet mellom en sirkels omkrets og diameteren.
π (uttalt «pie» og ofte skrevet «Pi») er en uendelig desimal med en felles tilnærming av 3.14159. Du kan finne ut mer om Pi her
Eksempel på beregning av arealet til en sirkel
 |
Area = πr2 Areal = 3.14159 x (4 cm) 2 Areal = 3.14159 x 16 cm2 Areal = 50.27 cm2 Svar avrundet til 2 desimaler |
Forklaring av området for en sirkelformel
Ta en sirkel og del den i like store sektorer og omorganisere disse som vist nedenfor. Legg merke til hvordan formene blir mer som et rektangel når sektorene blir mindre. Merk: Det er ingen grense for hvor små disse sektorene kan være og hvor tett de kan ligne et rektangel når de er ordnet.
Forutsatt at vi vet at omkretsen av en sirkel er lik 2πr, kan vi legge dimensjoner til «rektangelet» som vist nedenfor. Ved å bruke arealet til en formel for et rektangelareal, areal = bredde x høyde, kan vi se hvordan sirkelen vår, re-konfigurert som et rektangel, kan vises til å ha et areal som tilnærmer seg πr xr eller πr2 Sektorer omorganisert

Sirkelsektorer omorganisert – starter å se ut som et rektangel

Område for Sammensatte former
Det er mange tilfeller der beregningen av et totalt areal krever at mer enn ett område skal beregnes, etterfulgt av enten et tillegg, subtraksjon eller en annen kombinasjon av operasjoner for å finne ønsket område.
Merk: I eksemplene nedenfor vises ikke måleenhetene, og svar og verdien av π (Pi) er avrundet til nærmeste hundredel.
Eksempel: Enkle sammensatte former
Arealberegningseksemplet nedenfor er relativt enkelt. Formen kan sees på som en trekant kombinert med et rektangel.
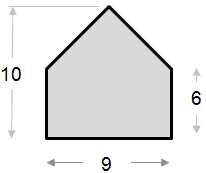 |
Areal av trekantdel: ½ x base x høyde ½ x 9 x 4 = 18 Areal til rektangeldelen: Totalt areal = 18 + 54 = 72 |
Eksemplet ovenfor illustrerer et vanlig krav når du arbeider med sammensatt figurer – finne dimensjoner som ikke er vist. Når du veileder barna dine, gi hjelp, når det er nødvendig, for å finne disse «manglende» dimensjonene. Det er et annet eksempel nedenfor.
Finne dimensjonene
 |
Hva er dimensjonene til den lille rektangulære delen? Bredde? 12 – 7 – 2 = 3 Høyde? 8 – 6 = 2 |
Eksempel: Å trekke ett område fra et annet
I eksemplet nedenfor kan formen ses som et rektangel med en trekant kuttet ut.
 |
Areal av rektangeldel: bredde x høyde 5 x 6 = 30 Areal av trekantdel: Totalt areal = 30 – 4,50 = 25,50 |
Eksempel: Delområder
Eksemplet nedenfor ligner på et over, men siden vi har en halvsirkel, må vi beregne en brøkdel (halvparten) av sirkelområdet. Merk i dette eksemplet at diameteren og ikke radiusen vises.
 |
Areal av trekantdel: ½ x base x høyde ½ x 6 x 6 = 18 Areal av halvcirkeldel: Totalt areal = 18 – 3,53 = 14,47 |
Eksempel: Avgjørelser! Kombinere? Trekk
Det er vanlig å ha mer enn én måte å beregne det endelige arealet på. I eksemplene nedenfor kan formen sees på som to rektangler kombinert eller som et stort rektangel med et mindre rektangel «kuttet ut» fra øverste høyre hjørne.
Beregning av arbeidsark
Skriv ut ut regnearkene som er oppført nedenfor, og bruk dem til praksis når du veileder barna dine.
- Beregning av områder – rektangler og firkanter
- Beregning av områder – rektangler
- Beregning Områder – Rektangler
- Beregning av sammensatte områder f.eks med rektangulære former
- Beregning av sammensatte områder f.eks. med rektangler, trekanter og sirkler
- Beregning av områder f.eks. av trekanter
- Areal av en sirkel
- Beregning av overflatearealer f.eks. av rektangulære prismer
Du finner flere utskrivbare regnearkark her.