Eksponensiell fordeling
av Marco Taboga, PhD
Den eksponensielle fordelingen er en kontinuerlig sannsynlighetsfordeling som brukes til modell tiden vi trenger å vente før en gitt hendelse inntreffer. Det er den kontinuerlige motstykket til den geometriske fordelingen, som i stedet er diskret.
Noen ganger kalles den også negativ eksponensiell fordeling.
Innledning
Hvor lang tid vil det gå før et jordskjelv inntreffer i en gitt region? Hvor lenge trenger vi å vente til en kunde kommer inn i butikken vår? Hvor lang tid tar det før et telefonsenter mottar neste telefonsamtale? Hvor lenge vil et stykke maskin fungere uten å bryte sammen?
Spørsmål som disse blir ofte besvart i sannsynlige termer ved å bruke den eksponensielle fordelingen.
Alle disse spørsmålene gjelder tiden vi trenger å vente før en gitt hendelse inntreffer. Hvis denne ventetiden er ukjent, er det ofte hensiktsmessig å tenke på den som en tilfeldig variabel som har en eksponensiell fordeling.
Grovt sett er tiden 
vi trenger å vente før en hendelse inntreffer har en eksponensiell fordeling hvis sannsynligheten for at hendelsen skjer i et bestemt tidsintervall er proporsjonal med lengden på det tidsintervallet.
Mer presist, har en eksponentiell fordeling hvis den betingede sannsynligheten er omtrent proporsjonal med lengden til tidsintervallet som ligger mellom tidene og , til enhver tid .
I mange praktiske situasjoner er denne egenskapen veldig realistisk. Dette er grunnen til at den eksponensielle fordelingen brukes så mye til å modellere ventetider.
Den eksponensielle fordelingen er strengt relatert til Poisson-fordelingen. Hvis 1) en hendelse kan inntreffe mer enn en gang og 2) tiden som har gått mellom to påfølgende forekomster er eksponensielt fordelt og uavhengig av tidligere forekomster, så har antall forekomster av hendelsen innen en gitt tidsenhet en Poisson-fordeling. Vi inviterer leseren til å se forelesningen om Poisson-distribusjonen for en mer detaljert forklaring og en intuitiv grafisk fremstilling av dette faktum.
Definisjon
Den eksponensielle fordelingen karakteriseres som følger.
Definisjon La være en kontinuerlig tilfeldig variabel. La støtten være settet med positive reelle tall: La . Vi sier at har en eksponentiell fordeling med parameter hvis og bare hvis sannsynlighetstetthetsfunksjonen er Parameteren kalles hastighetsparameter.
En tilfeldig variabel med en eksponensiell fordeling kalles også en eksponentiell tilfeldig variabel.
Det følgende er et bevis på at er en legitim sannsynlighetsdensitetsfunksjon.
Ikke-negativitet er åpenbar. Vi må bevise at integralen av over tilsvarer . Dette bevises som følger:
For å bedre forstå den eksponensielle fordelingen, kan du se på dens densitetsplott.
Hastighetsparameteren og dens tolkning
Vi har nevnt at sannsynligheten for at hendelsen skjer mellom to datoer og er proporsjonal med (betinget av at informasjonen ikke har skjedd før ). Hastighetsparameteren er proporsjonalitetskonstanten: der er uendelig høyere orden enn (dvs. en funksjon av som går til null raskere enn gjør).
Proporsjonalitetsbetingelsen ovenfor er også tilstrekkelig til å fullstendig karakterisere den eksponensielle fordelingen.
Proposition Proportionalitetsbetingelsen oppfylles bare hvis har en eksponentiell fordeling.
Den betingede sannsynligheten kan skrives som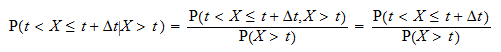 
Betegn med fordelingsfunksjonen til , det vil si og av dens overlevelsesfunksjon: Deretter Dele begge sider av , vi får der er en mengde som har en tendens til når har en tendens til . Tar grenser på begge sider, får vi eller, ved definisjonen av derivat: Denne differensiallikningen løses enkelt ved å bruke kjeden regel: Å ta integralet fra til på begge sider, får vi og eller Men (fordi ikke kan ta negative verdier) antyder Eksponentierende begge sider, får vi Derfor eller Men tetthetsfunksjonen er den første avledede av fordelingsfunksjonen: og begrepet lengst til høyre er tettheten til en eksponensiell tilfeldig variabel. Derfor oppfylles proporsjonalitetsbetingelsen bare hvis er en eksponentiell tilfeldig variabel
Forventet verdi
Den forventede verdien av en eksponentiell tilfeldig variabel er
Det kan avledes som følger: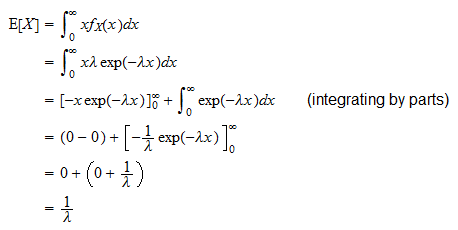 
Varians
Variansen til en eksponentiell tilfeldig variabel er
It kan avledes takket være den vanlige variansformelen (): 
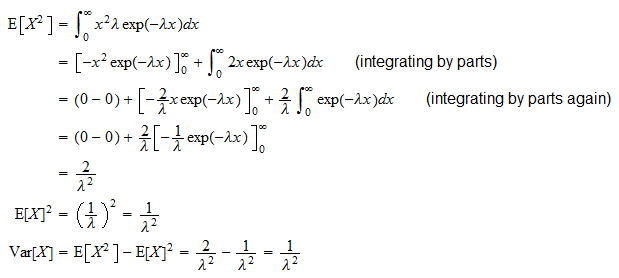
Momentgenererende funksjon
Momentgenereringsfunksjonen til en eksponentiell tilfeldig variabel er definert for alle :
Definisjonen av momentgenererende funksjon gir Av Selvfølgelig konvergerer de ovennevnte integralene bare hvis , dvs. bare hvis . Derfor eksisterer øyeblikksgenereringsfunksjonen til en eksponentiell tilfeldig variabel for alle .
Karakteristisk funksjon
Den karakteristiske funksjonen til en eksponentiell tilfeldig variabel er
Ved å bruke definisjonen av karakteristisk funksjon og det faktum at kan vi skrive Vi beregner nå de to integralene separat . Den første integralen er 
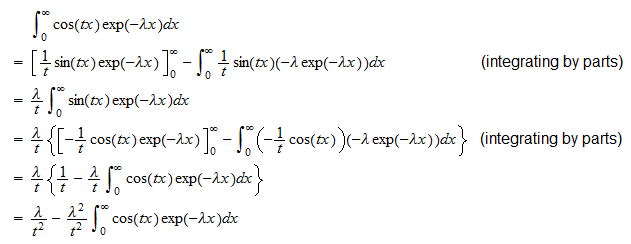Derfor som kan omorganiseres for å gi eller Den andre integralen er 
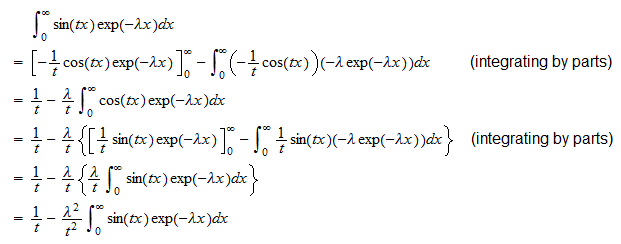Derfor som kan omorganiseres for å gi eller Ved å sette brikker sammen får vi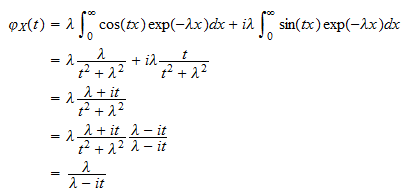 
Distribusjonsfunksjon
Distribusjonsfunksjonen til en eksponensiell tilfeldig variabel er
Hvis , så fordi kan ikke ta på seg negative verdier. Hvis , så
Flere detaljer
I de følgende underavsnittene kan du finne flere detaljer om den eksponentielle fordelingen.
Memoryless property
En av de viktigste egenskapene til den eksponentielle fordelingen er den memoryless egenskapen: for alle .
Dette bevises som følger: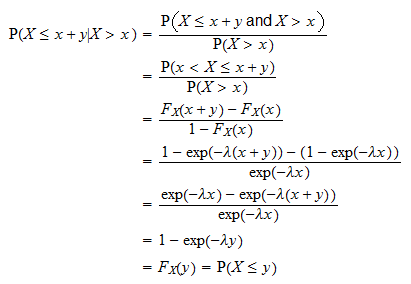 
er tiden vi trenger å vente før en bestemt hendelse inntreffer. Ovennevnte eiendom sier at sannsynligheten for at hendelsen skjer i et tidsintervall med lengde er uavhengig av hvor mye tid som allerede har gått () uten at hendelsen skjer.
Summen av eksponentielle tilfeldige variabler er en Gamma-tilfeldig variabel
Anta , , …, er gjensidig uavhengige tilfeldige variabler som har eksponentiell fordeling med parameter .
Definer
Så er summen en Gamma-tilfeldig variabel med parametere og .
Dette bevises ved hjelp av moment genererende funksjoner (husk at øyeblikksgenereringsfunksjonen til en sum av gjensidig uavhengige tilfeldige variabler bare er produktet av deres øyeblikksgenererende funksjoner): Sistnevnte er øyeblikksgenererende funksjon av en Gamma distribusjon med parametere og . Så har en gammafordeling, fordi to tilfeldige variabler har samme fordeling når de har samme øyeblikksgenererende funksjon.
Den tilfeldige variabelen sies også noen ganger å ha en Erlang-fordeling. Erlang-fordelingen er bare et spesielt tilfelle av gammadistribusjonen: en gammal tilfeldig variabel er også en tilfeldig Erlang-variabel når den kan skrives som en sum av eksponensielle tilfeldige variabler.
Tetthetsplott
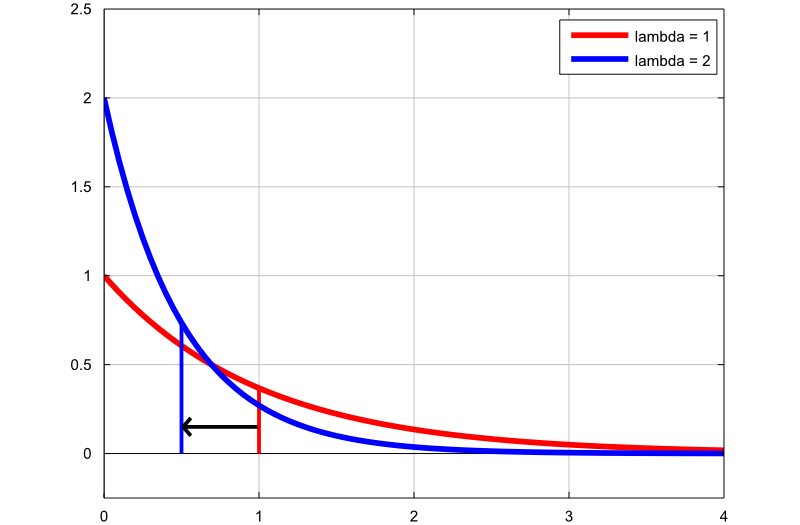
Neste plott viser hvordan tettheten til den eksponensielle fordelingen endres ved å endre hastighetsparameteren:
-
den første grafen (rød linje) er sannsynlighetstetthetsfunksjonen til en eksponensiell tilfeldig variabel med hastighetsparameter
; -
den andre grafen (blå linje) er sannsynlighetstetthetsfunksjonen til en eksponentiell tilfeldig variabel med hastighetsparameter
.
De tynne vertikale linjene indikerer middelverdiene for de to fordelingen. Merk at ved å øke hastighetsparameteren reduserer vi gjennomsnittet av fordelingen fra til .
Løst øvelser
Nedenfor kan du finne noen øvelser med forklarte løsninger.
Oppgave 1
La være en eksponentiell tilfeldig variabel med parameter . Beregn følgende sannsynlighet:
Først av alt kan vi skrive sannsynligheten som ved å bruke det faktum at sannsynligheten for at en kontinuerlig tilfeldig variabel får en bestemt verdi er lik null (se Kontinuerlige tilfeldige variabler og null-sannsynlighetshendelser). Nå kan sannsynligheten skrives i form av fordelingsfunksjonen til som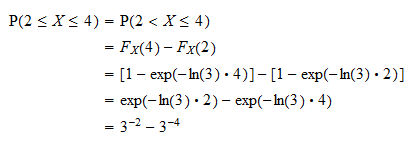 
Oppgave 2
Anta at den tilfeldige variabelen har en eksponensiell fordeling med parameteren . Beregn følgende sannsynlighet:
Denne sannsynligheten kan enkelt beregnes ved å bruke fordelingsfunksjonen til :
Oppgave 3
Hva er sannsynligheten for at en tilfeldig variabel er mindre enn forventet verdi, hvis har en eksponentiell fordeling med parameter ?
Den forventede verdien av en eksponentiell tilfeldig variabel med parameter er Sannsynligheten ovenfor kan beregnes ved å bruke fordelingsfunksjonen til :
Slik siterer du
Sitat som: