College Algebra
Læringsutbytte
- Identifiser toppunktet, symmetriaksen, y-skjæringspunktet, og minimum eller maksimumsverdien til en parabel fra det er graf.
- Identifiser en kvadratisk funksjon skrevet i generell og toppunktform.
- Gitt en kvadratisk funksjon i generell form, finn toppunktet.
- Definer domenet og rekkevidde for en kvadratisk funksjon ved å identifisere toppunktet som et maksimum eller minimum.
Grafen til en kvadratisk funksjon er en U-formet kurve som kalles en parabel. Et viktig trekk ved grafen er at den har et ekstremt punkt, kalt toppunktet. Hvis parabolen åpner seg, representerer toppunktet det laveste punktet på grafen, eller minimumsverdien til den kvadratiske funksjonen. Hvis parabolen åpner seg, representerer toppunktet det høyeste punktet i grafen, eller maksimumsverdien. I begge tilfeller er toppunktet et vendepunkt på grafen. Grafen er også symmetrisk med en vertikal linje tegnet gjennom toppunktet, kalt symmetriaksen.
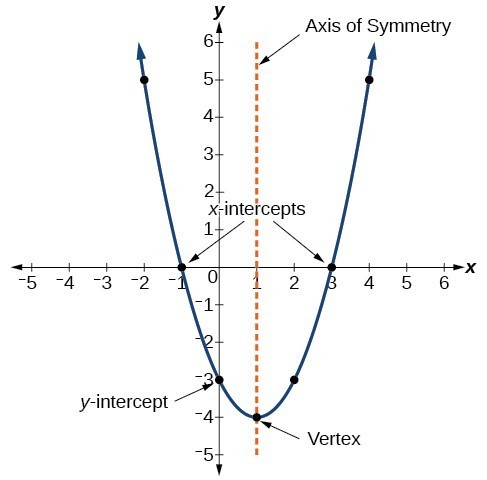
Ligninger av kvadratiske funksjoner
Den generelle formen for en kvadratisk funksjon presenterer funksjonen i formen
f \ left (x \ right) = a {x} ^ {2} + bx + c
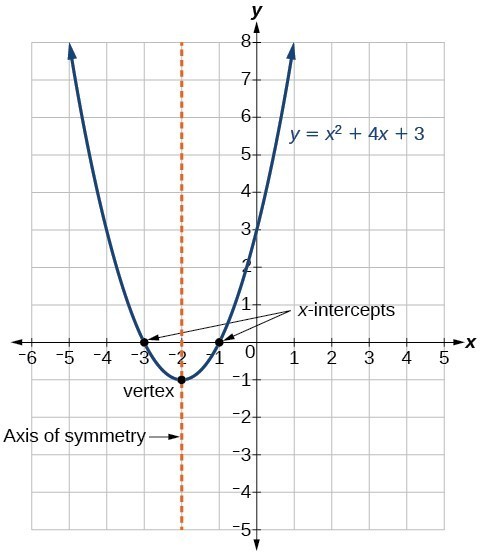
Standardformen for en kvadratisk funksjon presenterer funksjonen i skjemaet
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Gitt en kvadratisk funksjon generelt skjema, finn toppunktet til parabolen.
En grunn til at vi kanskje vil identifisere toppunktet til parabolen, er at dette punktet vil informere oss om hvor maksimums- eller minimumsverdien av utgangen skjer, k, og hvor det skjer, h. Hvis vi får den generelle formen for en kvadratisk funksjon:
f (x) = ax ^ 2 + bx + c
Vi kan definere toppunktet, (h, k), ved å gjøre følgende:
Finne domenet og rekkevidden til en kvadratisk funksjon
Ethvert tall kan være inngangsverdien til en kvadratisk funksjon. Derfor er domenet til enhver kvadratisk funksjon alle reelle tall. Fordi paraboler har et maksimum eller et minimum i toppunktet, er rekkevidden begrenset. Siden toppunktet til en parabel vil være enten et maksimum eller et minimum, vil området bestå av alle y-verdier større enn eller lik y-koordinaten til toppunktet eller mindre enn eller lik y-koordinaten ved vendepunktet , avhengig av om parabolen åpnes eller ned.
Bidra!
Forbedre denne sidenFinn ut mer