BFS vs DFS: Kjenn forskjellen

Hva er BFS ?

BFS er en algoritme som brukes til å tegne data eller søke i tre eller kryssende strukturer. Algoritmen besøker og markerer alle nøkkelknutene effektivt i en graf på en nøyaktig bredde.

Denne algoritmen velger en enkelt node (innledende eller kildepunkt) i en graf og besøker deretter alle nodene ved siden av den valgte noden. Når algoritmen besøker og merker startnoden, beveger den seg mot nærmeste ubesøkte noder og analyserer dem.

Når det er besøkt, blir alle noder markert. Disse gjentakelsene fortsetter til alle nodene i grafen har blitt besøkt og merket. Den fulle formen for BFS er det første søket etter bredde.

I denne BSF Vs. DFS Binary Tree tutorial, vil du lære:

• Hva er BFS?
• Hva er DFS?
• Eksempel på BFS
• Eksempel på DFS
• Forskjell mellom BFS og DFS binært tre
• Anvendelser av BFS
• Anvendelser av DFS

Hva er DFS?

DFS er en algoritme for å finne eller krysse grafer eller trær i dybderetningsretningen. Utførelsen av algoritmen begynner ved rotnoden og utforsker hver gren før tilbakesporing. Den bruker en stabeldatastruktur for å huske, for å få det påfølgende toppunktet, og for å starte et søk når en blindgate vises i en hvilken som helst iterasjon. Den fulle formen for DFS er dybde-første søk.

Eksempel på BFS

I det følgende eksemplet med DFS, vi har brukt graf som har 6 hjørner.

Eksempel på BFS

Trinn 1)

Du har en graf med syv tall fra 0 – 6.

Trinn 2)

0 eller null er merket som en rotnode.

Trinn 3)

0 er besøkt, merket , og satt inn i kødatastrukturen.

Trinn 4)

Gjenværende 0 tilstøtende og ikke besøkt noder besøkes, merkes og settes inn i køen.

Trinn 5)

Gjennomgang av gjentakelser gjentas til alle noder besøkes.

Eksempel på DFS

I det følgende eksemplet på DFS har vi brukt en ikke-rettet graf som har 5 hjørner.

Trinn 1)

Vi har startet fra toppunkt 0. Algoritmen begynner med å sette den i den besøkte listen og samtidig sette alle de tilstøtende toppunktene i dataene struktur kalt stack.

Trinn 2)

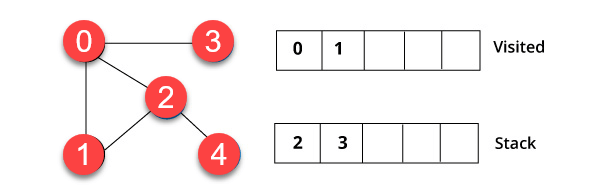
Du besøker elementet , som er på toppen av bunken, for eksempel 1 og går til de tilstøtende noder. Det er fordi 0 allerede er besøkt. Derfor besøker vi toppunkt 2.

Trinn 3)

Vertex 2 har et ubesøkt nærliggende toppunkt i 4. Derfor legger vi til det i stabelen og besøker det.

Trinn 4)

Til slutt vil vi besøke siste toppunkt 3 har den ikke ubesøkte tilstøtende noder. Vi har fullført traverseringen av grafen ved hjelp av DFS-algoritme.

Forskjell mellom BFS og DFS binært tre

BFS	DFS
BFS finner den korteste veien til destinasjonen.	DFS går til bunnen av et undertre, og deretter backtracks .
Den fulle BFS-formen er Breadth-First Search.	Den fulle DFS-formen er Depth First Search.
Den bruker en kø for å holde rede på neste sted å besøke.	Den bruker en stabel for å holde rede på neste sted å besøke.
BFS krysser i henhold til trenivå.	DFS krysser i henhold til tredybde.
Den er implementert ved hjelp av FI FO-liste.	Den er implementert ved hjelp av LIFO-listen.
Det krever mer minne sammenlignet med DFS.	Det krever mindre minne sammenlignet med BFS.
Denne algoritmen gir den grunne baneløsningen.	Denne algoritmen garanterer ikke den grunne løsningen.
Det er ikke behov for backtracking i BFS.	Det er et behov for tilbakesporing i DFS.
Du kan aldri bli fanget i endelige løkker.	Du kan bli fanget i uendelige løkker.
Hvis du ikke finner noe mål, kan det hende du må utvide mange noder før løsningen blir funnet.	Hvis du ikke finner noe mål, kan tilbakesporing av bladnoden kanskje skje.

Applikasjoner av BFS

Her er applikasjoner av BFS:

Uvektet Grafer:

BFS-algoritme kan enkelt opprette den korteste banen og et minimum spennende tre for å besøke alle hjørnene i grafen på kortest mulig tid med høy nøyaktighet.

P2P-nettverk:

BFS kan implementeres for å finne alle nærmeste eller nærliggende noder i et peer-to-peer-nettverk. Dette vil finne de nødvendige dataene raskere.

Web-crawlere:

Søkemotorer eller web-crawlere kan enkelt bygge flere nivåer av indekser ved å bruke BFS. BFS-implementering starter fra kilden, som er nettsiden, og deretter besøker den alle koblingene fra den kilden.

Nettverkssending:

En kringkastet pakke styres av BFS-algoritmen for å finne og nå alle nodene den har adressen til.

Anvendelser av DFS

Her er viktige anvendelser av DFS:

Vektet graf:

I en vektet graf genererer DFS-grafgjennomgang det korteste stitreet og minimumstreet.

Oppdage en syklus i en graf:

En graf har en syklus hvis vi fant en bakkant under DFS. Derfor bør vi kjøre DFS for grafen og kontrollere for bakkanter.

Path Finding:

Vi kan spesialisere oss i DFS-algoritmen for å søke en bane mellom to hjørner.

Topologisk sortering:

Den brukes primært til å planlegge jobber fra de gitte avhengighetene blant arbeidsgruppene. I datavitenskap brukes den i instruksjonsplanlegging, dataserialisering, logisk syntese, bestemmer rekkefølgen på kompileringsoppgaver.

Søker etter sterkt koblede komponenter i en graf:

Den brukes i DFS-graf når det er en bane fra hvert toppunkt i grafen til andre gjenværende toppunkt.

Løs oppgaver med bare én løsning:

DFS-algoritme kan enkelt tilpasses for å søke i alle løsninger til en labyrint ved å inkludere noder på den eksisterende banen i det besøkte settet.