クイックソートアルゴリズム
クイックソートは、分割統治の概念に基づいた別のソート手法の1つです。マージソート。しかし、クイックソートでは、配列をサブ配列に分割するときにすべての面倒な作業(主要な作業)が行われますが、マージソートの場合、実際の作業はすべてサブ配列のマージ中に行われます。クイックソートの場合、結合ステップはまったく何もしません。
これはパーティション交換ソートとも呼ばれます。このアルゴリズムは、リストを3つの主要部分に分割します。
- ピボット要素よりも小さい要素
- ピボット要素(中央要素)
- よりも大きい要素ピボット要素
ピボット要素は、配列の任意の要素にすることができ、最初の要素、最後の要素、または任意のランダム要素にすることができます。このチュートリアルでは、右端の要素または最後の要素をピボットとして使用します。
例:配列{52, 37, 63, 14, 17, 8, 6, 25}では、。したがって、最初のパスの後、リストは次のように変更されます。
{6 8 17 14 25 63 37 52}
したがって、最初のパスの後、ピボットはその位置に設定され、すべての要素が左側に小さくなり、すべての要素が右側より大きくなります。これで、6 8 17 14と63 37 52は2つの別個のサンアレイと見なされ、同じ再帰ロジックが適用されます。これは、次のようになるまで続けます。配列全体がソートされます。
クイックソートの仕組み
クイックソートアルゴリズムに関連する手順は次のとおりです。
- 要素を次のように選択した後この場合、配列の最後のインデックスであるピボットは、配列を初めて分割します。
- クイックソートでは、これをパーティショニングと呼びます。配列を2つのサブ配列に分割するのは簡単ではありませんが、分割する場合、配列要素は、ピボットよりも小さいすべての要素がピボットの左側にあり、ピボットよりも大きいすべての要素がピボットの左側にあるように配置されます。
- ピボット要素は最終的に並べ替えられた位置になります。
- 左右の要素は並べ替えられない場合があります。
- 次に、サブ配列、ピボットの左側の要素、ピボットの右側の要素を選択し、サブ配列のピボットを選択してそれらのパーティション化を実行します。
値を持つ配列を考えてみましょう{9, 7, 5, 11, 12, 2, 14, 3, 10, 6}
以下に、指定された配列をクイックソートでソートする方法を図で表したものです。
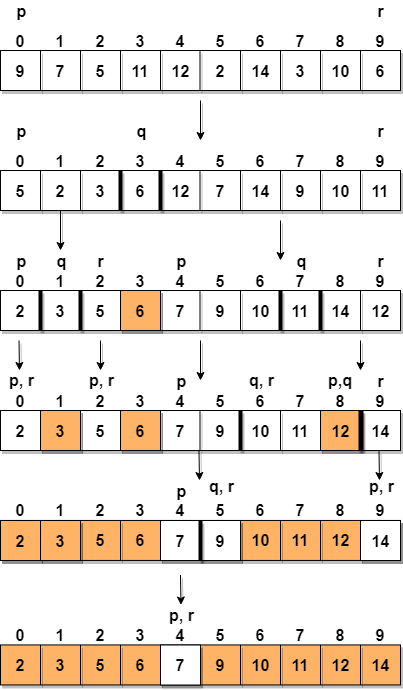
ステップ1では、最後の要素をピボット(この場合は6)、およびpartitioningを呼び出すため、再配置しますg 6が最終位置に配置され、左側にそれよりも小さいすべての要素が配置され、右側にすべての要素が配置されるように配列を指定します。
次に、左側のサブアレイと右側のサブアレイを選択し、それらのピボットを選択します。上の図では、3左側のサブアレイのピボットとして、11右側のサブアレイのピボットとして。
そして、もう一度partitioning。
クイックソートアルゴリズムの実装
以下に、クイックソートアルゴリズムを実装する単純なCプログラムがあります。

クイックソートの複雑さの分析
パーティション化によってサブアレイが不均衡になり、左側に要素がなく、すべての要素が含まれる配列の場合ピボットよりも大きいため、右側にあります。
そして、不均衡なサブ配列を取得し続ける場合は、実行最悪の場合、O(n2)
分割によってほぼ等しいサブ配列が生成される場合と同様に、実行時間は最良であり、時間計算量は次のようになります。 O(n * log n)。
最悪の場合の時間計算量:O(n2)
最良の場合の時間計算量:O(n * log n)
平均時間計算量:O(n * log n)
空間計算量:O(n * log n)
今知っているように、サブアレイの分割が分割後に生成された場合バランスが悪いと、クイックソートが完了するまでに時間がかかります。最後のインデックスを常にピボットとして選択することを誰かが知っている場合、意図的に配列を提供することができます。これにより、クイックソートの最悪の場合の実行時間が発生します。
これを回避するには、ランダムに選択します。ピボット要素も。アルゴリズムに違いはありません。必要なのは、配列からランダムな要素を選択し、それを最後のインデックスの要素と交換し、ピボットにして、クイックソートを続行することだけです。
- クイックソートに必要なスペースは非常に少なく、
O(n*log n)の追加スペースのみが必要です。 - クイックソートは安定したソート手法ではないため、ソート中にリスト内の2つの類似した要素の出現を変更する可能性があります。
これでクイックソートについて学習しました。 アルゴリズムについては、これらの並べ替えアルゴリズムとそのアプリケーションも確認できます。
- 挿入並べ替え
- 選択並べ替え
- バブル並べ替え
- マージソート
- ヒープソート
- カウントソート