Algoritmo di ordinamento rapido

Lordinamento rapido è una delle diverse tecniche di ordinamento che si basa sul concetto di Divide and Conquer, proprio come unisci ordinamento. Ma nellordinamento rapido tutto il lavoro pesante (lavoro principale) viene svolto dividendo larray in sottoarray, mentre in caso di merge sort, tutto il lavoro reale avviene durante lunione dei sottoarray. In caso di ordinamento rapido, il passaggio di combinazione non fa assolutamente nulla.

È anche chiamato ordinamento con scambio di partizioni. Questo algoritmo divide lelenco in tre parti principali:

1. Elementi minori dellelemento Pivot
2. Elemento Pivot (elemento centrale)
3. Elementi maggiori dellelemento elemento pivot

Lelemento pivot può essere qualsiasi elemento dellarray, può essere il primo elemento, lultimo elemento o qualsiasi elemento casuale. In questo tutorial, prenderemo lelemento più a destra o lultimo elemento come pivot.

Ad esempio: Nellarray {52, 37, 63, 14, 17, 8, 6, 25}, prendiamo 25 come pivot. Quindi, dopo il primo passaggio, lelenco verrà modificato in questo modo.

{6 8 17 14 25 63 37 52}

Quindi, dopo il primo passaggio, il pivot verrà impostato nella sua posizione, con tutti gli elementi più piccoli alla sua sinistra e tutti gli elementi più grandi che alla sua destra. Ora 6 8 17 14 e 63 37 52 sono considerati come due sunarrays separati e su di essi verrà applicata la stessa logica ricorsiva e continueremo a farlo finché viene ordinato larray completo.

Come funziona lordinamento rapido?

Di seguito sono riportati i passaggi coinvolti nellalgoritmo di ordinamento rapido:

1. Dopo aver selezionato un elemento come pivot, che nel nostro caso è lultimo indice dellarray, dividiamo larray per la prima volta.
2. Nellordinamento rapido, chiamiamo questo partizionamento. Non è semplice suddividere un array in 2 sottoarray, ma in caso di partizionamento, gli elementi dellarray sono posizionati in modo che tutti gli elementi più piccoli del pivot si trovino sul lato sinistro del pivot e tutti gli elementi maggiori del pivot lo saranno essere sul lato destro di esso.
3. E lelemento pivot sarà nella sua posizione ordinata finale.
4. Gli elementi a sinistra ea destra, potrebbero non essere ordinati.
5. Quindi selezioniamo i sottoarray, gli elementi a sinistra del pivot e gli elementi a destra del pivot, ed eseguiamo il partizionamento su di essi scegliendo un pivot nei sottoarray.

Consideriamo un array con valori {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

Di seguito, abbiamo una rappresentazione grafica di come lordinamento veloce ordinerà larray dato.

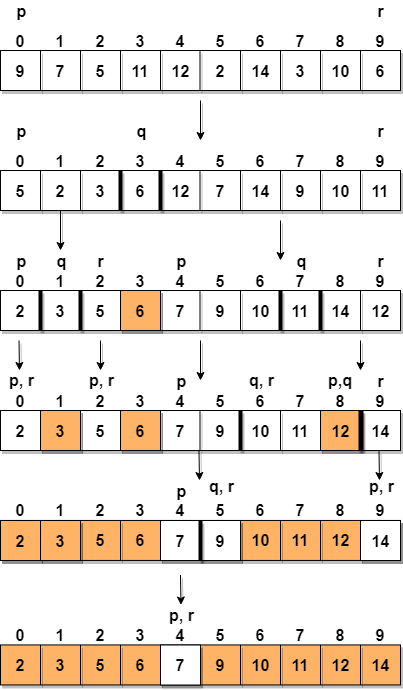
Nel passaggio 1, selezioniamo lultimo elemento come pivot, che in questo caso è 6 e chiama partitioning, quindi riorganizza g larray in modo tale che 6 sarà posto nella sua posizione finale e alla sua sinistra ci saranno tutti gli elementi meno di esso e alla sua destra avremo tutti gli elementi maggiore di esso.

Quindi scegliamo il sottoarray a sinistra e il sottoarray a destra e selezioniamo un pivot per loro, nel diagramma sopra, abbiamo scelto 3 come perno per il sottoarray sinistro e 11 come perno per il sottoarray destro.

E chiamiamo di nuovo partitioning.

Implementazione dellalgoritmo di ordinamento rapido

Di seguito abbiamo un semplice programma in C che implementa lalgoritmo di ordinamento rapido:

Analisi della complessità dellordinamento rapido

Per un array, in cui il partizionamento porta a sottoarray sbilanciati, in una misura in cui sul lato sinistro non ci sono elementi, con tutti gli elementi maggiore del pivot, quindi sul lato destro.

E se continui a ottenere sottoarray sbilanciati, la corsa ning il tempo è il caso peggiore, che è O(n2)

Dove come se il partizionamento portasse a sottoarray quasi uguali, il tempo di esecuzione è il migliore, con la complessità del tempo O (n * log n).

Complessità tempo caso peggiore: O (n2)

Complessità tempo caso migliore: O (n * log n)

Complessità temporale media: O (n * log n)

Complessità spaziale: O (n * log n)

Come sappiamo ora, il partizionamento dei sottoarray prodotto dopo il partizionamento sono sbilanciati, lordinamento rapido impiegherà più tempo per terminare. Se qualcuno sa che scegli sempre lultimo indice come pivot, può intenzionalmente fornirti un array che si tradurrà in un tempo di esecuzione nel peggiore dei casi per lordinamento rapido.

Per evitare ciò, puoi scegliere casuale anche lelemento pivot. Non farà alcuna differenza nellalgoritmo, poiché tutto ciò che devi fare è scegliere un elemento casuale dallarray, scambiarlo con lelemento nellultimo indice, renderlo il pivot e continuare con lordinamento rapido.

• Lo spazio richiesto dallordinamento rapido è molto inferiore, è richiesto solo O(n*log n) spazio aggiuntivo.
• Lordinamento rapido non è una tecnica di ordinamento stabile, quindi potrebbe cambiare la presenza di due elementi simili nellelenco durante lordinamento.

Ora che abbiamo imparato lordinamento rapido algoritmo, puoi controllare anche questi algoritmi di ordinamento e le loro applicazioni:

• Ordinamento di inserzione
• Ordinamento di selezione
• Ordinamento a bolle
• Unisci ordinamento
• Ordinamento heap
• Ordinamento conteggio