Gyors rendezés algoritmus

A Gyors rendezés a különféle rendezési technikák egyike, amely a Divide and Conquer koncepciójára épül, akárcsak egyesítés rendezés. A gyorsválogatás során azonban az összes nehéz emelés (fő munka) a tömb alsávokra osztása közben történik, míg egyesítéses rendezés esetén az összes valós munka az alsávok összevonása során történik. Gyors rendezés esetén a kombinációs lépés semmit sem tesz.

Partíciócsere-rendezésnek is nevezik. Ez az algoritmus három fő részre osztja a listát:

1. Kevesebb, mint a Pivot elem
2. Pivot elem (Central elem)
3. A pivot elem

A pivot elem tetszőleges elem lehet a tömbből, lehet első, utolsó vagy bármilyen véletlenszerű elem. Ebben az oktatóanyagban a jobb szélső elemet vagy az utolsó elemet vesszük el pivotként.

Például: A {52, 37, 63, 14, 17, 8, 6, 25} tömbben 25 pivotként. Tehát az első lépés után a lista így módosul.

{6 8 17 14 25 63 37 52}

Ennélfogva az első menet után a forgást a helyére állítják, balra az összes kisebb elem, jobbra pedig az összes nagyobb lesz. Most a 6 8 17 14 és a 63 37 52 két különálló napsugárnak tekintjük, és ugyanaz a rekurzív logika lesz alkalmazva rajtuk, és ezt addig folytatjuk, amíg a teljes tömb rendezve van.

Hogyan működik a gyors rendezés?

Az alábbiakban bemutatjuk a gyors rendezési algoritmus lépéseit:

1. Miután kiválasztott egy elemet pivot, amely esetünkben a tömb utolsó indexe, először osztjuk fel a tömböt.
2. Gyors rendezésben ezt partíciónak hívjuk. Nem egyszerű a tömb 2 részsávra bontása, de particionálás esetén a tömbelemek olyan helyzetben vannak, hogy az összes, a csuklónál kisebb elem a csukló bal oldalán lesz, és a csuklónál nagyobb elemek legyen a jobb oldalán.
3. És a forgó elem a végső rendezett helyzetben lesz.
4. A bal és jobb oldali elemek nem rendezhetők.
5. Ezután kiválasztunk részsávokat, elemeket a forgás bal oldalán és elemeket a forgás jobb oldalán, és partíciót hajtunk végre rajtuk úgy, hogy kiválasztunk egy csuklót az alsávokban.

Vegyünk egy tömböt {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}

értékekkel az alábbiakban: képi ábrázolás arról, hogy a gyors rendezés hogyan rendezi az adott tömböt.

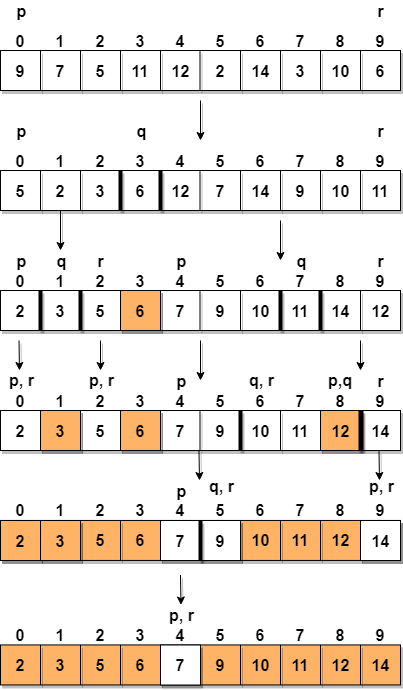
Az 1. lépésben az utolsó elemet választjuk ki pivot, ami ebben az esetben 6, és felhívja a partitioning parancsot, ezért rendezze újra g a tömböt oly módon, hogy 6 a végső helyzetbe kerüljön, balra pedig az összes elem kevesebb legyen nála és jobbra, minden elemünk meg lesz nagyobb, mint ez.

Ezután a bal és a jobb oldali részképet választjuk, és kiválasztunk egy pivotot a fenti ábrán a 3 pivotként a bal alrészhez és 11 mint pivot a jobb oldali alrészhez.

És ismét felhívjuk a partitioning.

Gyorsrendezés algoritmusának megvalósítása

Az alábbiakban egy egyszerű C programmal rendelkezünk, amely a Gyors rendezés algoritmust valósítja meg:

Gyors rendezés összetettségének elemzése

Olyan tömb esetén, amelyben a particionálás kiegyensúlyozatlan részsávokhoz vezet, olyan mértékben, ahol a bal oldalon nincsenek elemek, az összes elemgel nagyobb, mint a forgás, tehát a jobb oldalon.

És ha továbbra is kiegyensúlyozatlan részsávok jelennek meg, akkor a futás A legrosszabb eset az idő, amely O(n2)

Ahol a particionálás majdnem egyenlő részsávokhoz vezet, akkor a futási idő a legjobb, az idő összetettségével O (n * log n).

Legrosszabb eset időbeli összetettsége: O (n2)

Legjobb eset időbeli összetettsége: O (n * log n)

Átlagos időbeli komplexitás: O (n * log n)

Térbonyolultság: O (n * log n)

Mint azt már tudjuk, hogy ha a partícionálás után előállított partíciók részcsíkok kiegyensúlyozatlanok, a gyors rendezés több időt vesz igénybe. Ha valaki tudja, hogy az utolsó indexet állandóan pivotként választja, szándékosan megadhatja a tömböt, amely a legrosszabb futási időt eredményezi a gyors rendezéshez.

Ennek elkerülése érdekében választhat véletlenszerű forgó elem is. Nem fog különbséget tenni az algoritmusban, mivel csak annyit kell tennie, hogy kiválaszt egy véletlenszerű elemet a tömbből, felcseréli az utolsó indexen lévő elemmel, elforgatja és gyors rendezéssel folytatja.

• A gyors rendezéshez szükséges hely nagyon kevés, csak O(n*log n) további hely szükséges.
• A gyors rendezés nem stabil válogatási technika, ezért megváltoztathatja két hasonló elem előfordulását a listában a rendezés során.

Most, hogy megtanultuk a gyors rendezést algoritmus, megnézheti ezeket a rendezési algoritmusokat és azok alkalmazását is:

• Beszúrás rendezése
• Kiválasztás rendezése
• Buborék rendezése
• Rendezés egyesítése
• Halom rendezés
• Rendezés számlálása