Mesure: découverte de formules pour laire

Formules daire

Élèves qui ont la notion informelle que laire est la « quantité de 2-D «substance» »contenue à lintérieur dune région peut inventer pour elle-même la plupart des formules quon leur demande souvent simplement de mémoriser. Chaque formule quils réinventent contribue à renforcer leur compréhension (et leur mémoire) des autres formules quils connaissent. (Voir aussi surface.)

Zone de rectangles

En choisissant un carré comme unité de surface, nous obtenons une idée intuitive de la surface des rectangles. Si nous décidons que laire de ce carré est 1, alors un rectangle 7 fois plus long aurait 7 × 1 comme son aire.

Un rectangle qui est deux fois la hauteur de aurait deux fois sa superficie, donc laire de est 2 × 7 unités de surface. On peut compter les deux rangées de sept carrés. De même, comporte 3 lignes de 7 carrés (ou 7 colonnes de 3 carrés), pour un total de 7 × 3 carrés, donc sa superficie est de 21 unités carrées.

Le nombre de carrés dans une ligne correspond à la longueur du rectangle. Le nombre de lignes correspond à la hauteur du rectangle. La zone est donc longueur × hauteur.

Puisquun rectangle peut être dessiné de manière oblique, « hauteur » est défini comme signifiant « la direction perpendiculaire à la base » et « base » est définie comme suit: enfin, quel que soit le côté que vous choisissez.

Cela fonctionne pour compter les nombres. Cela fonctionne même pour les fractions. 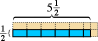Le rectangle bleu montré ici mesure la moitié unité de longueur de haut par cinq unités et demie de longueur. Si nous choisissons le carré correspondant comme unité de surface, nous voyons que le rectangle bleu contient cinq demi-unités de surface et un quart dunité de surface, soit un total de deux et trois quarts unités de surface. (Les parties roses indiquent lachèvement de chaque unité de surface carrée.)

Pour inclure tous les nombres, nous définissons laire dun rectangle comme étant la base × la hauteur (où « base » et « hauteur » désignent les longueurs de ces côtés, mesurées dans les mêmes unités).

Aire de parallélogrammes

Obtenir lidée

Nous pouvons trouver une formule pour laire dun parallélogramme par dissection le parallélogramme et réorganiser les pièces pour créer un rectangle. Le parallélogramme et le rectangle étant composés des mêmes parties, ils ont nécessairement la même aire. (Voir la définition de la zone pour en savoir plus sur les raisons pour lesquelles ces zones sont identiques.)

Nous pouvons voir quelles ont également exactement la même longueur de base (bleu) et exactement la même hauteur (vert). Parce que base × hauteur donne laire du rectangle, nous pouvons utiliser les mêmes mesures sur le parallélogramme pour calculer son aire: base × hauteur. (Comme précédemment, « hauteur » est mesurée perpendiculairement à la base et « base » est le côté que vous avez choisi en premier. Voir le parallélogramme.)

La coupe ci-dessus permet de voir facilement que la longueur de base est inchangé. En fait, la coupe perpendiculaire peut être faite nimporte où le long de la base.

Étaiement des trous

Intuition et preuve

Cette dissection donne une compréhension intuitive de la formule de laire pour un parallélogramme, une raison pour laquelle il devrait être ce quil est. Mais nous ne nous sommes pas demandé si la dissection «fonctionne» vraiment. Autrement dit, lorsque nous coupons le parallélogramme et réorganisons ses parties, nous nous attendons à obtenir et le résultat ressemble certainement à cela. Mais les apparences peuvent être trompeuses. Quest-ce qui nous garantit que lorsque nous déplaçons ce triangle, le résultat est un rectangle? Et sil ressemble plus à (bien que moins exagéré)? Si le résultat nest pas toujours un rectangle parfait, nous ne pouvons pas utiliser notre connaissance de la formule de laire du rectangle pour développer une formule pour le parallélogramme. Au lycée, les élèves pourront prouver que les deux parties du parallélogramme, une fois réassemblées correctement, font un rectangle . De la maternelle à la 8e année, pour la plupart, les élèves doivent sappuyer sur lexpérience visuelle et avoir une impression intuitive. En savoir plus sur les raisons pour lesquelles ces dissections fonctionnent.

Et si nous choisissons le côté court comme base?

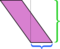
Nous sommes libres de choisir nimporte quel côté comme base; « hauteur » est défini comme étant mesurée perpendiculairement au côté que nous choisissons comme base. Si nous prenons le côté court (bleu) comme base, la dissection illustrée ci-dessus n’est pas aussi convaincante. Couper le long de cette altitude et réorganiser les pièces laisse un désordre:

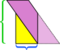
Dans cet exemple particulier, nous pouvons sauver le désordre en faisant une autre coupe, 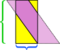mais que se passerait-il si le parallélogramme était encore plus long et plus mince?

Il savère que tout parallélogramme, quelle que soit sa longueur et sa finesse, peut être disséqué de cette manière afin que les parties – peut-être beaucoup dentre elles – puissent être réorganisées en un rectangle. Mais il faut plus de travail pour montrer que cela peut toujours être fait. Nous avons besoin dune autre idée.

Une idée de dissection légèrement différente rend la vie beaucoup plus facile dans ce cas. (Vous pouvez montrer par vous-même que cela fonctionne également dans le cas dorigine.)

• Encadrez le parallélogramme dans un rectangle.
• Les deux parties du rectangle qui ne sont pas à lintérieur du parallélogramme sont des triangles congruents.
• Faites glisser lun de ces triangles vers lautre jusquà ce quils se rencontrent pour former un rectangle. 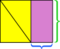Parce que la surface totale du rectangle extérieur na pas changé (cest le même rectangle quavant) et que la zone jaune na pas changé (les pièces viennent de bouger), la différence entre eux – les zones violettes – doivent être les mêmes. Comme précédemment, nous pouvons également voir que les dimensions de la zone rectangulaire violette sont la base et la hauteur du parallélogramme dorigine.

Intuition et preuve, reprise : Encore une fois, la dissection fournit les informations essentielles, mais il faut un peu plus de travail pour sassurer que les deux triangles jaunes, qui semblent certainement semboîtent pour former un rectangle, sadaptent vraiment précisément, et pas seulement presque.

Pourquoi est-il important dêtre si prudent?

Lorsque nous construisons dautres formules daires (ci-dessous), nous voudrons utiliser notre comment trouver laire dun parallélogramme, et donc nous voulons pour pouvoir compter sur la règle que nous avons trouvée. Nous pouvons être sûrs que la réorganisation des pièces ne change pas la zone: cest, après tout, comment nous définissons la zone. Mais nous devons également nous assurer que les pièces s’emboîtent comme nous le prétendons, sinon nous ne pouvons pas nous fier aux mesures que nous avons effectuées. Et nous devons être sûrs que la règle base × hauteur ne dépend pas dun choix chanceux de base.

Dans la plupart des programmes, les élèves nont pas une base suffisamment systématique de connaissances géométriques avant la 8e année pour faire des preuves solides que ces dissections fonctionnent. Mais la compréhension intuitive est suffisante pour expliquer et justifier les formules, et une bonne base pour une étude géométrique ultérieure.

Aire du triangle

Savoir comment trouver laire dun parallélogramme nous aide trouver laire dun triangle.

Dissection du triangle

Nous pouvons disséquer le triangle en deux parties – lune delles un triangle, et lautre un trapèze – en le coupant parallèlement à la base. Si nous coupons la hauteur exactement de moitié avec cette tranche, les deux parties semboîtent pour former un parallélogramme avec la même base mais la moitié de la hauteur.

Donc base × demi-hauteur donne laire du triangle. Une dissection similaire montre une demi-base × hauteur. Lun ou lautre se réduit à bh.

Doubler le triangle puis diviser par deux la surface résultante

Une autre façon de penser: deux copies de le triangle forme un parallélogramme de même base et de même hauteur que le triangle.

Laire du parallélogramme est base × hauteur, mais cest deux fois laire du triangle, donc laire du triangle est de base × hauteur, comme nous lavons vu avec la méthode de dissection.

(Comme toujours , choisissez une «base» et mesurez la hauteur perpendiculaire à cette base, de la base au sommet opposé.)

Aire du trapèze

Doubler le trapèze puis diviser par deux laire résultante

Comme pour le triangle, deux copies dun trapèze peuvent être assemblées pour former un parallélogramme.

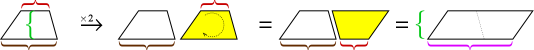
La hauteur du parallélogramme est la même que la hauteur du trapèze, mais sa base est la somme des deux bases du trapèze. La surface du parallélogramme est donc la hauteur × (base1 + base2). Mais cette zone est composée de deux trapèzes, nous devons donc la couper en deux pour obtenir la zone du trapèze.

Dissection du trapèze

Nous pourrions également disséquer le trapèze comme nous lavons disséqué le triangle, avec une seule tranche coupant sa hauteur de moitié. Les deux parties semboîtent pour former un parallélogramme dont la base est la somme des deux bases du trapèze, mais dont la hauteur est la moitié de la hauteur du trapèze.

Dans le cas du trapèze, les bases ne peuvent pas être choisi à volonté. Les deux côtés parallèles sont les bases et la hauteur, comme toujours, est la distance perpendiculaire dune base à lautre.

Laire de ce parallélogramme est sa hauteur (mi-hauteur du trapèze) multipliée par sa base (somme des bases du trapèze), donc son aire est mi-hauteur × (base1 + base2). Parce que le parallélogramme est fait exactement de la même «substance» que le trapèze, cest aussi la zone du trapèze.

De toute façon, la zone du trapèze est × hauteur × (base1 + base2).

Aire dautres quadrilatères spéciaux

Aire de losange

Laire dun losange peut être trouvée en coupant et en réarrangeant les pièces pour former un parallélogramme. Cela peut être fait de plusieurs manières:

1. Coupez à travers la diagonale plus courte (a) pour former deux triangles congruents. Déplacez la moitié inférieure du triangle à côté de la moitié supérieure pour former un parallélogramme. La diagonale la plus courte (a) devient la base du parallélogramme, et la moitié de la diagonale la plus longue (b) devient la hauteur du parallélogramme. Ainsi, laire du losange est a * b ou le produit des diagonales, qui est la formule standard du losange.
2. Une autre manière similaire consiste à couper le losange en quatre triangles congruents et à les réorganiser en un rectangle avec la diagonale la plus courte comme base et la moitié de la diagonale la plus longue comme hauteur.
3. Après la coupe le losange en deux triangles congruents, nous pouvons calculer laire de lun des triangles, qui est * base (a) * hauteur ( b) = ab. Multipliez ensuite par deux car il y en a deux: 2 * ab = ab.

Zone du cerf-volant

La zone dun cerf-volant peut être trouvée similaire à la zone dun losange. Couper à travers la diagonale plus longue donne deux triangles congruents. Si nous les réorganisons, nous pouvons former un parallélogramme avec la diagonale la plus longue (b) comme base et la moitié de la diagonale la plus courte (a) comme hauteur. Ainsi, la zone devient b * a = ab. Une approche plus compliquée implique un peu dalgèbre. Coupez le cerf-volant sur la diagonale la plus courte pour former deux triangles avec la diagonale la plus courte (a) comme base. Ainsi, laire du premier triangle est a * squiggly, où squiggly est la hauteur. Laire du deuxième triangle est a * (b – squiggly), où (b – squiggly) est la partie restante de la diagonale la plus longue. La surface totale devient ainsi ( a * squiggly) + ( a * (b – squiggly)). En tenant compte de a, nous avons a (squiggly + b – squiggly) = ab.

Eh bien, que savez-vous. Fondamentalement, il vous suffit de connaître la formule pour laire dun parallélogramme, puis de dériver la formule pour les autres.