Distribution exponentielle
par Marco Taboga, PhD
La distribution exponentielle est une distribution de probabilité continue utilisée pour modéliser le temps quil faut attendre avant quun événement donné se produise. Cest la contrepartie continue de la distribution géométrique, qui est plutôt discrète.
Parfois, on lappelle aussi distribution exponentielle négative.
Introduction
Combien de temps sécoulera-t-il avant quun tremblement de terre ne se produise dans une région donnée? Combien de temps faut-il attendre quun client entre dans notre boutique? Combien de temps faudra-t-il avant quun centre dappels reçoive le prochain appel téléphonique? Combien de temps une machine fonctionnera-t-elle sans tomber en panne?
Des questions comme celles-ci sont fréquemment répondues en termes probabilistes en utilisant la distribution exponentielle.
Toutes ces questions concernent le temps dont nous avons besoin dattendre avant quun événement donné ne se produise. Si ce temps dattente est inconnu, il convient souvent de le considérer comme une variable aléatoire ayant une distribution exponentielle.
En gros, le temps 
dont nous avons besoin attendre avant quun événement ne se produise a une distribution exponentielle si la probabilité que lévénement se produise pendant un certain intervalle de temps est proportionnelle à la longueur de cet intervalle de temps.
Plus précisément, a une distribution exponentielle si la probabilité conditionnelle est approximativement proportionnelle à la longueur de lintervalle de temps compris entre les heures et , à tout instant .
Dans de nombreuses situations pratiques, cette propriété est très réaliste. Cest la raison pour laquelle la distribution exponentielle est si largement utilisée pour modéliser les temps dattente.
La distribution exponentielle est strictement liée à la distribution de Poisson. Si 1) un événement peut se produire plus dune fois et 2) le temps écoulé entre deux occurrences successives est distribué exponentiellement et indépendamment des occurrences précédentes, alors le nombre doccurrences de lévénement dans une unité de temps donnée a une distribution de Poisson. Nous invitons le lecteur à voir la conférence sur la distribution de Poisson pour une explication plus détaillée et une représentation graphique intuitive de ce fait.
Définition
La distribution exponentielle est caractérisée comme suit.
Définition Soit une variable aléatoire continue. Soit son support lensemble des nombres réels positifs: Soit . On dit que a une distribution exponentielle avec le paramètre si et seulement si sa fonction de densité de probabilité est Le paramètre est appelé paramètre de débit.
Une variable aléatoire ayant une distribution exponentielle est également appelée variable aléatoire exponentielle.
Ce qui suit est une preuve que est une fonction de densité de probabilité légitime.
La non-négativité est évidente. Nous devons prouver que lintégrale de sur est égale à . Ceci est prouvé comme suit:
Pour mieux comprendre la distribution exponentielle, vous pouvez jeter un œil à ses graphiques de densité.
Le paramètre rate et son interprétation
Nous avons mentionné que la probabilité que lévénement se produise entre deux dates et est proportionnel à (conditionnel à ce que cela ne se soit pas produit avant ). Le paramètre de taux est la constante de proportionnalité: où est un nombre infinitésimal de dordre supérieur à (cest-à-dire une fonction de qui passe à zéro plus rapidement que fait).
La condition de proportionnalité ci-dessus est également suffisante pour caractériser complètement la distribution exponentielle.
Proposition La condition de proportionnalité nest satisfait que si a une distribution exponentielle.
La probabilité conditionnelle peut sécrire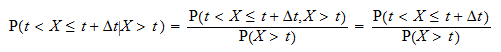 
Désignons par la fonction de distribution de , cest-à-dire et par sa fonction de survie: Puis, Divisant les deux côtés par , nous obtenons où est une quantité qui tend vers lorsque tend vers . En prenant des limites de part et dautre, on obtient ou, par la définition de dérivée: Cette équation différentielle se résout facilement en utilisant la chaîne règle: En prenant lintégrale de à des deux côtés, nous obtenons et ou Mais (car ne peut pas prendre de valeurs négatives) implique En exposant les deux côtés, nous obtenons Par conséquent, ou Mais la fonction de densité est la première dérivée de la fonction de distribution: et le terme le plus à droite est la densité dune variable aléatoire exponentielle. Par conséquent, la condition de proportionnalité nest satisfaite que si est une variable aléatoire exponentielle
Valeur attendue
La valeur attendue dune variable aléatoire exponentielle est
Il peut être dérivé comme suit: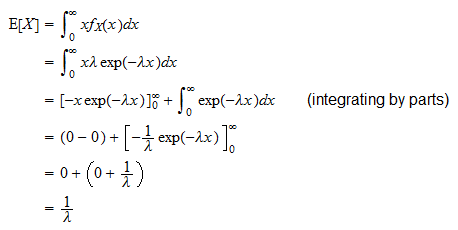 
Variance
La variance dun variable aléatoire exponentielle est
Il peut être dérivée grâce à la formule de variance habituelle (): 
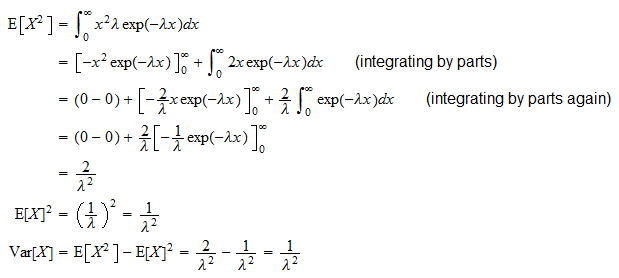
Fonction de génération de moment
La fonction de génération de moment dune variable aléatoire exponentielle est définie pour tout :
La définition de la fonction de génération de moment donne De Bien entendu, les intégrales ci-dessus ne convergent que si , cest-à-dire uniquement si . Par conséquent, la fonction de génération de moment dune variable aléatoire exponentielle existe pour tout .
Fonction caractéristique
La fonction caractéristique dune variable aléatoire exponentielle est
En utilisant la définition de la fonction caractéristique et le fait que nous pouvons écrire Nous calculons maintenant séparément les deux intégrales . La première intégrale est 
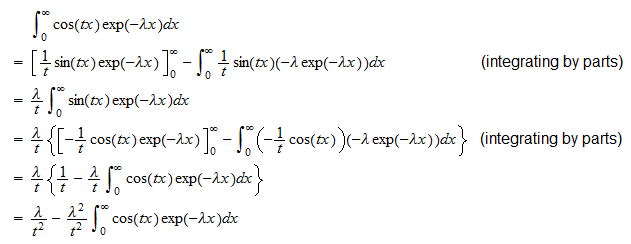Par conséquent, qui peut être réorganisée pour donner ou La deuxième intégrale est 
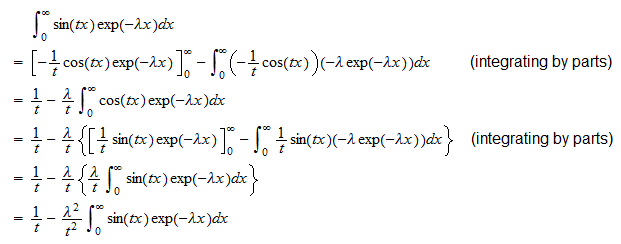Par conséquent, qui peut être réorganisée pour donner ou En assemblant les pièces, nous obtenons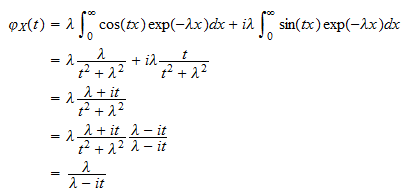 
Fonction de distribution
La fonction de distribution dune variable aléatoire exponentielle est
Si , alors car ne peut pas prendre de valeurs négatives. Si , alors
Plus de détails
Dans les sous-sections suivantes, vous pouvez trouver plus de détails sur la distribution exponentielle.
Propriété sans mémoire
Lune des propriétés les plus importantes de la distribution exponentielle est la propriété sans mémoire: pour tout .
Ceci est prouvé comme suit: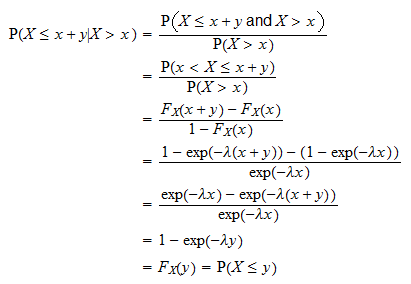 
est le temps quil faut attendre avant un certain événement se produit. La propriété ci-dessus indique que la probabilité que lévénement se produise pendant un intervalle de temps de longueur est indépendante du temps qui sest déjà écoulé () sans que lévénement ne se produise.
La somme des variables aléatoires exponentielles est une variable aléatoire Gamma
Supposons , , …, sont des variables aléatoires mutuellement indépendantes ayant une distribution exponentielle avec le paramètre .
Définissez
Ensuite, la somme est une variable aléatoire Gamma avec des paramètres et .
Ceci est prouvé en utilisant le moment fonctions génératrices de moments (rappelez-vous que la fonction génératrice de moments dune somme de variables aléatoires mutuellement indépendantes est juste le produit de leurs fonctions génératrices de moments): Cette dernière est la fonction génératrice de moments dun Gamma distribution avec les paramètres et . Donc, a une distribution Gamma, car deux variables aléatoires ont la même distribution quand elles ont la même fonction génératrice de moment.
La variable aléatoire est aussi parfois dite avoir une distribution dErlang. La distribution dErlang nest quun cas particulier de la distribution Gamma: une variable aléatoire Gamma est également une variable aléatoire dErlang lorsquelle peut être écrite comme une somme de variables aléatoires exponentielles.
Diagramme de densité
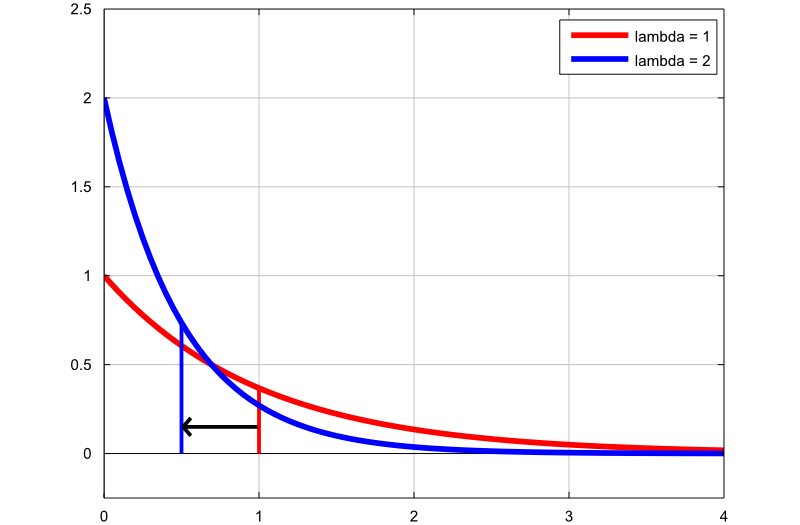
Le graphique suivant montre comment la densité de la distribution exponentielle change en modifiant le paramètre de taux:
-
le premier graphique (ligne rouge) est la fonction de densité de probabilité dune variable aléatoire exponentielle avec le paramètre de taux
; -
le deuxième graphique (ligne bleue) est la fonction de densité de probabilité dune variable aléatoire exponentielle avec le paramètre de taux
.
Les fines lignes verticales indiquent les moyennes des deux distributions. Notez quen augmentant le paramètre de taux, nous diminuons la moyenne de la distribution de à .
Exercices résolus
Vous trouverez ci-dessous quelques exercices avec des solutions expliquées.
Exercice 1
Soit une variable aléatoire exponentielle avec le paramètre . Calculez la probabilité suivante:
Tout dabord, nous pouvons écrire la probabilité sous la forme en utilisant le fait que la probabilité quune variable aléatoire continue prenne une valeur spécifique est égale à zéro (voir Variables aléatoires continues et événements à probabilité nulle). Maintenant, la probabilité peut être écrite en fonction de la fonction de distribution de comme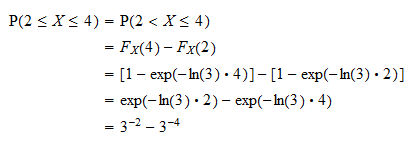 
Exercice 2
Supposons que la variable aléatoire a une distribution exponentielle avec le paramètre . Calculez la probabilité suivante:
Cette probabilité peut être facilement calculée en utilisant la fonction de distribution de :
Exercice 3
Quelle est la probabilité quune variable aléatoire est inférieur à sa valeur attendue, si a une distribution exponentielle avec le paramètre ?
La valeur attendue dune variable aléatoire exponentielle avec le paramètre est La probabilité ci-dessus peut être calculée en utilisant la fonction de distribution de :
Comment citer
Veuillez citer comme suit: