Distribution de Poisson
Étant donné un processus de Poisson, la probabilité dobtenir exactement 
succès dans les essais 
est donnée par la limite dune distribution binomiale
 |
(1)
|
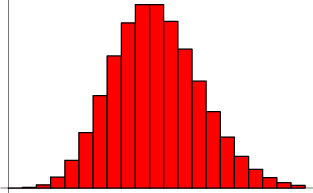
Visualisation de la distribution en fonction du nombre de succès attendu
 |
(2)
|
au lieu de la taille de léchantillon 
pour 
fixe, léquation (2) devient alors
 |
(3)
|
En laissant la taille de léchantillon 
devenir grande, la distribution se rapproche alors
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
qui est connue sous le nom de distribution de Poisson (Papoulis 1984, pp. 101 et 554; Pfeiffer et Schum 1973, p. 200). Notez que la taille de léchantillon 
a complètement disparu de la fonction de probabilité, qui a la même forme fonctionnelle pour toutes les valeurs de 
.
La distribution de Poisson est implémentée dans le WolframLanguage comme PoissonDistribution.
Comme prévu, la distribution de Poisson est normalisée de sorte que la somme des probabilités soit égale à 1, puisque
 |
(9 )
|
Le rapport des probabilités est donné par
 |
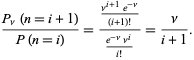(10)
|
La distribution de Poisson atteint un maximum lorsque
 |
(11)
|
où est la constante dEuler-Mascheroni et 
est un nombre harmonique, conduisant à léquation transcendantale
 |
(12)
|
qui ne peut pas être résolu exactement pour 
.
La fonction de génération de moment de la distribution Poisson est donnée par
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
donc
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, p. 554).
Les moments bruts peuvent également être calculés directement par sommation, ce qui donne une connexion inattendue avec le polynôme de Bell 
et les nombres de Stirling du second type,
 |
(21)
|
connue sous le nom de formule de Dobiński.Par conséquent,
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
Les moments centraux peuvent alors être calculés comme
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
donc la moyenne, la variance, lasymétrie et lexcès daplatissement sont
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
La fonction caractéristique de la distribution Poissond est
(Papoulis 1984, p. 154 et 554), et la fonction de génération de cumulant est
 |
(34)
|
donc
 |
(35)
|
Lécart moyen de la distribution de Poisson est donné par
 |
(36)
|
La distribution de Poisson peut également être exprimée en termes de
 |
(37)
|
 |
(38)
|
La fonction génératrice de moment dune distribution de Poisson en deux variables est donnée par
 |
(39)
|
Si les variables indépendantes 
, 
, …, 
ont des distributions de Poisson avec des paramètres 
, 
, …, 
, puis
 |
(40)
|
a une distribution de Poisson avec paramètre
 |
(41)
|
Ceci peut être vu puisque la fonction de génération de cumulants est
 |
(42)
|
 |
(43)
|
Une généralisation de la distribution de Poisson a été utilisée par Saslaw (1989) pour modéliser le regroupement observé de galaxies dans lunivers. La forme de cette distribution est donnée par
 |
(44)
|
où 
est le nombre de galaxies dans un volume 
, 
, 
est la densité moyenne des galaxies, et 
, avec 
est le rapport de lénergie gravitationnelle à la cinétique énergie de mouvements particuliers, Laisser 
donner
 |
(45)
|
qui est en effet une distribution de Poisson avec 
. De même, laisser 
donne 
.