Comment calculer laire

Calculer laire

Laire est mesurée en carrés (ou unités carrées).

Combien de carrés y a-t-il dans ce rectangle?

Nous pouvons compter les carrés ou nous pouvons prenez la longueur et la largeur et utilisez la multiplication. Le rectangle ci-dessus a une aire de 15 unités carrées.

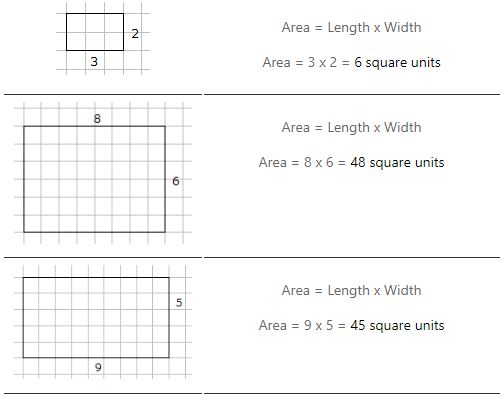
Laire dun rectangle est = longueur x largeur

Exemples de calcul de laire dun rectangle

Unités de mesure de la zone

Nous mesurons la zone en utilisant des carrés. Nous utilisons différentes tailles de carrés selon la taille dune zone.

Exemple	Longueur de côté sur les carrés	Unité
Taille du ongle sur votre pouce	Millimètre	mm2
Taille de la feuille de papier	Centimètre	cm2
Taille dune pièce	Mètre	m2
Taille dune ville	Kilomètre	km2

Noubliez pas le petit 2

Nous écrivons les tailles carrées en utilisant un petit 2 à côté de lunité.
Nous écrivons mm2, cm2, m2, km2, cm2
Nous pouvons dire « 63 millimètres carrés » ou « 63 millimètres carrés »

Nous pourrions utiliser de petits carrés pour mesurer de grandes surfaces. Le seul problème avec ceci est que nous finirions par devoir utiliser de très gros Nombres. Par exemple, un champ pourrait être mesuré à 5 000 000 000 de millimètres carrés alors que 5 000 mètres carrés seraient une taille beaucoup plus facile à dire, à écrire et à visualiser.

Vous entendrez probablement plus dunités pour mesurer la zone; pouces carrés, pieds carrés, yards carrés, miles carrés, acres, hectares sont toutes des unités utilisées pour mesurer la superficie.

Autres exemples de calcul de la superficie

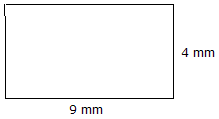	Aire = Longueur x Largeur Aire = 9 mm x 4 mm = 36 mm2
	Aire = Longueur x Largeur Aire = 7 cm x 6 cm = 42 cm2
	Aire = Longueur x Largeur Aire = 8 mx 2 m = 16 m2
	Aire = Longueur x Largeur Aire = 7 km x 5 km = 35 km2

Aire dun carré

La longueur et la largeur dun carré sont les mêmes, il suffit donc de multiplier la longueur par la longueur.

Aire = Longueur x Longueur Aire = 6 cm x 6 cm = 36 cm2

Aire dun cercle

Laire dun cercle = πr2
où r est le rayon du cercle et π est le rapport entre la circonférence dun cercle et son diamètre.

π (prononcé « tarte » et souvent écrit « Pi ») est une décimale infinie avec un commun approximation de 3,14159. Vous pouvez en savoir plus sur Pi ici

Exemple de calcul de laire dun cercle

Area = πr2 Area = 3,14159 x (4 cm) 2 Superficie = 3,14159 x 16 cm2 Superficie = 50,27 cm2 Réponse arrondie à 2 décimales

Explication de la formule de laire dun cercle

Prenez un cercle et divisez-le en secteurs de taille égale et réorganisez-les comme indiqué ci-dessous. Remarquez comment, à mesure que les secteurs deviennent plus petits, la forme ressemble davantage à un rectangle. Remarque: Il ny a pas de limite à la taille de ces secteurs et à la façon dont ils pourraient ressembler à un rectangle lorsquils sont disposés.

En supposant que nous savons que la circonférence dun cercle est égale à 2πr, nous pouvons ajouter des dimensions à le « rectangle » comme indiqué ci-dessous. En utilisant la formule daire dun rectangle, aire = largeur x hauteur, nous pouvons voir comment notre cercle, reconfiguré en rectangle, peut être montré comme ayant une aire qui se rapproche de πr xr ou πr2

Cercle Secteurs réorganisés

Secteurs de cercle réorganisés – Début ressembler à un rectangle

Superficie de Formes composées

Il existe de nombreux cas où le calcul dune surface totale nécessite le calcul de plusieurs surfaces, suivies dune addition, dune soustraction ou dune autre combinaison dopérations pour trouver la surface requise.

Remarque: Dans les exemples ci-dessous, les unités de mesure ne sont pas affichées et les réponses et la valeur de π (Pi) ont été arrondies au centième près.

Exemple: Formes composées simples

Lexemple de calcul daire ci-dessous est relativement simple. La forme peut être vue comme un triangle combiné avec un rectangle.

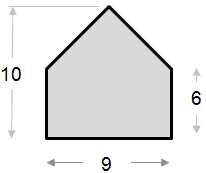Aire de la partie triangulaire: ½ x base x hauteur ½ x 9 x 4 = 18 Aire de la partie rectangle: largeur x hauteur 9 x 6 = 54 Aire totale = 18 + 54 = 72

Lexemple ci-dessus illustre une exigence courante lorsque vous travaillez avec des composés formes – recherche de dimensions non affichées. Lors du tutorat de vos enfants, aidez, si nécessaire, à trouver ces dimensions «manquantes». Voici un autre exemple ci-dessous.

Recherche des dimensions

Quelles sont les dimensions de la petite partie rectangulaire? Largeur? 12 – 7 – 2 = 3 Hauteur? 8 – 6 = 2

Exemple: soustraire une zone dune autre

Dans lexemple ci-dessous, la forme peut être vue comme un rectangle avec un triangle découpé.

Aire de la partie rectangle: largeur x hauteur 5 x 6 = 30 Aire de la partie triangle: ½ x base x hauteur ½ x 3 x 3 = 4,50 Superficie totale = 30 – 4.50 = 25.50

Exemple: aires partielles

Lexemple ci-dessous est similaire à celui ci-dessus bien que, puisque nous avons un demi-cercle, nous devons calculer une fraction (un demi) de laire du cercle « . Notez dans cet exemple que le diamètre, et non le rayon, est indiqué.

Aire de la partie triangle: ½ x base x hauteur ½ x 6 x 6 = 18 Aire de la partie demi-cercle: ½ x (πr2) ½ x (3.14 x 1,52) = 3,53 Superficie totale = 18 – 3,53 = 14,47

Exemple: décisions! Combiner? Soustraire

Il est courant davoir plus dune façon de calculer la surface finale. Dans les exemples ci-dessous, la forme peut être vue comme deux rectangles combinés ou comme un grand rectangle avec un rectangle plus petit « découpé » dans le coin supérieur droit.

Calcul des feuilles de calcul de la zone

Imprimer Extrayez les feuilles de travail ci-dessous et utilisez-les pour vous entraîner lors du tutorat de vos enfants.

• Calcul des surfaces – Rectangles et carrés
• Calcul des surfaces – Rectangles
• Calcul Surfaces – Rectangles
• Calcul des surfaces composées, par exemple avec des formes rectangulaires
• Calcul des surfaces composées, par ex. avec des rectangles, des triangles et des cercles
• Calcul des aires, par ex. de triangles
• Aire dun cercle
• Calcul daires de surface, par ex. des prismes rectangulaires

Vous trouverez plus de feuilles de calcul de géométrie imprimables ici.