BFS vs DFS: Connaissez la différence

Quest-ce que BFS ?

BFS est un algorithme utilisé pour représenter graphiquement des données ou rechercher des arbres ou traverser des structures. Lalgorithme visite et marque efficacement tous les nœuds clés dans un graphique de manière précise dans le sens de la largeur.

Cet algorithme sélectionne un seul nœud (point initial ou source) dans un graphique, puis visite tous les nœuds adjacents au nœud sélectionné. Une fois que lalgorithme visite et marque le nœud de départ, il se déplace vers les nœuds non visités les plus proches et les analyse.

Une fois visités, tous les nœuds sont marqués. Ces itérations se poursuivent jusquà ce que tous les nœuds du graphe aient été visités et marqués avec succès. La forme complète de BFS est la recherche en largeur dabord.

Dans ce BSF Vs. Didacticiel sur larbre binaire DFS, vous apprendrez:

• Quest-ce que BFS?
• Quest-ce que DFS?
• Exemple de BFS
• Exemple de DFS
• Différence entre BFS et DFS Binary Tree
• Applications de BFS
• Applications de DFS

Quest-ce que DFS?

DFS est un algorithme pour trouver ou parcourir des graphiques ou des arbres dans le sens de la profondeur. Lexécution de lalgorithme commence au nœud racine et explore chaque branche avant de revenir en arrière. Il utilise une structure de données de pile pour se souvenir, pour obtenir le sommet suivant et pour démarrer une recherche, chaque fois quune impasse apparaît dans une itération. La forme complète de DFS est la recherche en profondeur dabord.

Exemple de BFS

Dans lexemple suivant de DFS, nous ont utilisé un graphe ayant 6 sommets.

Exemple de BFS

Étape 1)

Vous avez un graphique de sept nombres allant de 0 à 6.

Étape 2)

0 ou zéro a été marqué comme nœud racine.

Étape 3)

0 est visité, marqué et inséré dans la structure de données de la file dattente.

Étape 4)

0 restant adjacent et non visité les nœuds sont visités, marqués et insérés dans la file dattente.

Étape 5)

Les itérations de déplacement sont répétées jusquà ce que tous les nœuds sont visités.

Exemple de DFS

Dans lexemple suivant de DFS, nous avons utilisé un graphe non orienté ayant 5 sommets.

Étape 1)

Nous sommes partis du sommet 0. Lalgorithme commence par le mettre dans la liste visitée et en mettant simultanément tous ses sommets adjacents dans les données structure appelée pile.

Étape 2)

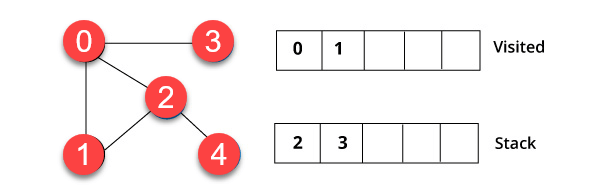
Vous visiterez lélément , qui se trouve en haut de la pile, par exemple, 1 et accédez à ses nœuds adjacents. Cest parce que 0 a déjà été visité. Par conséquent, nous visitons le sommet 2.

Étape 3)

Vertex 2 a un sommet voisin non visité en 4. Par conséquent, nous ajoutons cela dans la pile et le visitons.

Étape 4)

Enfin, nous visiterons le dernier sommet 3, il na pas de nœuds adjacents non visités. Nous avons terminé le parcours du graphe en utilisant lalgorithme DFS.

Différence entre larbre binaire BFS et DFS

BFS	DFS
BFS trouve le chemin le plus court vers la destination.	DFS va au bas dun sous-arbre, puis revient en arrière .
La forme complète de BFS est Breadth-First Search.	La forme complète de DFS est Depth First Search.
Il utilise une file dattente pour suivre le prochain emplacement à visiter.	Il utilise une pile pour garder une trace du prochain emplacement à visiter.
BFS parcourt selon le niveau de larborescence.	DFS parcourt selon la profondeur de larborescence.
Il est implémenté en utilisant FI Liste FO.	Il est implémenté en utilisant la liste LIFO.
Il nécessite plus de mémoire par rapport à DFS.	Il nécessite moins de mémoire que BFS.
Cet algorithme donne la solution de chemin le moins profond.	Cet algorithme ne garantit pas la solution de chemin le moins profond.
Il n’ya pas besoin de retour arrière dans BFS.	Il y a un besoin de retour en arrière dans DFS.
Vous ne pouvez jamais être piégé dans des boucles finies.	Vous pouvez être piégé dans des boucles infinies.
Si vous ne trouvez aucun objectif, vous devrez peut-être développer de nombreux nœuds avant que la solution ne soit trouvée.	Si vous ne trouvez aucun objectif, le retour arrière du nœud feuille peut se produire.

Applications de BFS

Voici les applications de BFS:

Non pondéré Graphiques:

Lalgorithme BFS peut facilement créer le chemin le plus court et un arbre couvrant minimum pour visiter tous les sommets du graphe dans les plus brefs délais avec une grande précision.

Réseaux P2P:

BFS peut être implémenté pour localiser tous les nœuds les plus proches ou voisins dans un réseau peer to peer. Cela trouvera les données requises plus rapidement.

Web Crawlers:

Les moteurs de recherche ou les robots Web peuvent facilement créer plusieurs niveaux dindex en utilisant BFS. La mise en œuvre de BFS commence à partir de la source, qui est la page Web, puis elle visite tous les liens de cette source.

Diffusion réseau:

Un paquet diffusé est guidé par lalgorithme BFS pour trouver et atteindre tous les nœuds pour lesquels il a ladresse.

Applications de DFS

Voici les applications importantes de DFS:

Graphique pondéré:

Dans un graphe pondéré, le parcours de graphe DFS génère larbre de chemin le plus court et larbre couvrant minimum.

Détection dun cycle dans un graphique:

Un graphique a un cycle si nous trouvons un bord arrière pendant DFS. Par conséquent, nous devons exécuter DFS pour le graphique et vérifier les arêtes arrière.

Recherche de chemin:

Nous pouvons nous spécialiser dans lalgorithme DFS pour rechercher un chemin entre deux sommets.

Tri topologique:

Il est principalement utilisé pour planifier des travaux à partir des dépendances données dans le groupe de travaux. En informatique, il est utilisé dans la planification des instructions, la sérialisation des données, la synthèse logique, la détermination de lordre des tâches de compilation.

Recherche de composants fortement connectés dun graphe:

Il est utilisé dans le graphe DFS quand il y a un chemin de chaque sommet du graphe vers dautres sommets restants.

Résoudre des énigmes avec une seule solution:

Lalgorithme DFS peut être facilement adapté pour rechercher toutes les solutions dun labyrinthe en incluant des nœuds sur le chemin existant dans lensemble visité.