Algèbre universitaire
Résultats dapprentissage
- Identifier le sommet, laxe de symétrie, lordonnée à lorigine et la valeur minimale ou maximale dune parabole à partir de cest un graphe.
- Identifiez une fonction quadratique écrite sous forme générale et de sommet.
- Étant donné une fonction quadratique sous forme générale, trouvez le sommet.
- Définissez le domaine et la plage dune fonction quadratique en identifiant le sommet comme maximum ou minimum.
Le graphique dune fonction quadratique est une courbe en forme de U appelée parabole. Une caractéristique importante du graphe est quil a un point extrême, appelé le sommet. Si la parabole souvre, le sommet représente le point le plus bas du graphique, ou la valeur minimale de la fonction quadratique. Si la parabole souvre vers le bas, le sommet représente le point le plus élevé du graphique, ou la valeur maximale. Dans les deux cas, le sommet est un point tournant sur le graphique. Le graphique est également symétrique avec une ligne verticale tracée à travers le sommet, appelée axe de symétrie.
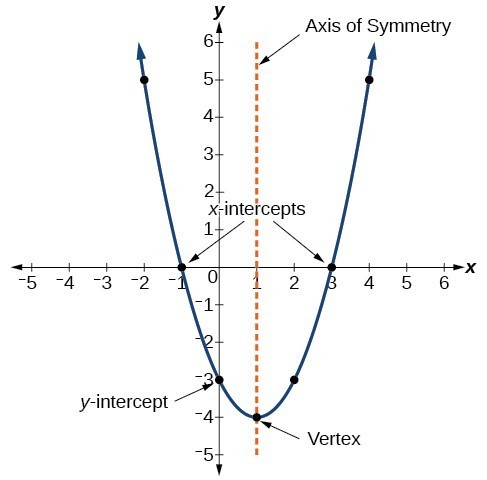
Equations des fonctions quadratiques
La forme générale dune fonction quadratique présente la fonction sous la forme
f \ left (x \ right) = a {x} ^ {2} + bx + c
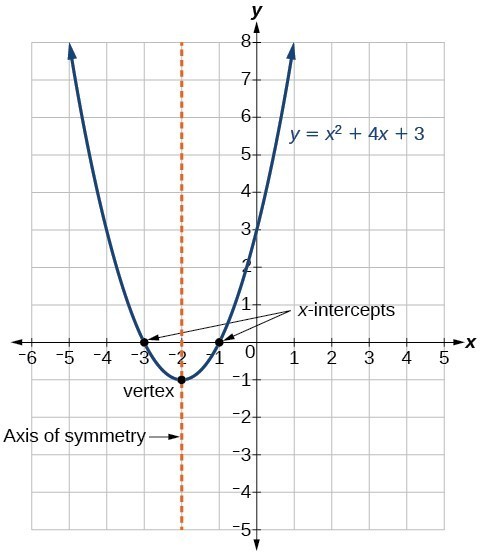
La forme standard dune fonction quadratique présente la fonction sous la forme
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Étant donné une fonction quadratique en général forme, trouvez le sommet de la parabole.
Une des raisons pour lesquelles nous pouvons vouloir identifier le sommet de la parabole est que ce point nous informera où la valeur maximale ou minimale de la sortie se produit, k, et où cela se produit, h. Si on nous donne la forme générale dune fonction quadratique:
f (x) = ax ^ 2 + bx + c
On peut définir le sommet, (h, k), en procédant comme suit:
Recherche du domaine et de la plage dune fonction quadratique
Tout nombre peut être la valeur dentrée dune fonction quadratique. Par conséquent, le domaine de toute fonction quadratique est tous les nombres réels. Comme les paraboles ont un maximum ou un minimum au sommet, la plage est restreinte. Étant donné que le sommet dune parabole sera soit un maximum, soit un minimum, la plage sera constituée de toutes les valeurs y supérieures ou égales à la coordonnée y du sommet ou inférieures ou égales à la coordonnée y au point de retournement , selon que la parabole souvre vers le haut ou vers le bas.
Contribuez!
Améliorez cette pageEn savoir plus