Poisson-jakauma
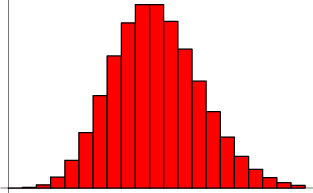
Poisson-prosessin perusteella todennäköisyys saada tarkalleen 
menestys 
-tutkimuksissa saadaan binomijakauman rajasta
 |
(1)
|
Jakauman tarkastelu odotettujen onnistumisten määrän funktiona
 |
(2)
|
näytekoon kiinteälle 
, yhtälöstä (2) tulee sitten
 |
(3)
|
Annetaan otoksen koon 
suureksi, jakauma lähestyy sitten
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
joka tunnetaan nimellä Poisson-jakauma (Papoulis 1984, s. 101 ja 554; Pfeiffer ja Schum 1973, s. 200). Huomaa, että otoksen koko 
on pudonnut kokonaan todennäköisyysfunktiosta, jolla on sama toiminnallinen muoto kaikille arvoille 
.
Poisson-jakauma toteutetaan WolframLanguagessa PoissonDistribution-nimisenä.
Odotetusti Poisson-jakauma normalisoidaan siten, että todennäköisyyksien summa on 1, koska
 |
(9 )
|
Todennäköisyyksien suhde saadaan seuraavasti:
 |
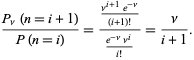(10)
|
Poisson-jakauma saavuttaa maksimiarvon, kun
 |
(11)
|
missä on Euler-Mascheronin vakio ja 
on harmoninen luku, joka johtaa transsendenttiseen yhtälöön
 |
(12)
|
jota ei voida ratkaista tarkalleen kohteelle 
.
Poisson-jakauman hetken tuottava funktio saadaan
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
joten
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, s. 554).
Raakamomentit voidaan laskea myös suoraan summaamalla, mikä antaa odottamattoman yhteyden Bellin polynomiin 
ja toisenlaisiin Stirling-numeroihin,
 |
(21)
|
tunnetaan Dobińskin kaavana.Siksi
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
Tällöin keskeiset hetket voidaan laskea nimellä
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
joten keskiarvo, varianssi, vinous ja kurtosiksen ylimäärä ovat
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
Poissondistributionin ominaisuusfunktio on
(Papoulis 1984, s. 154 ja 554), ja kumulantteja tuottava toiminto on
 |
(34)
|
joten
 |
(35)
|
Poissonin jakauman keskimääräinen poikkeama saadaan
 |
(36)
|
Poisson-jakauma voidaan ilmaista myös sanoilla
 |
(37)
|
 |
(38)
|
aPoisson-jakauman hetkenluova funktio kahdessa muuttujassa saadaan seuraavasti:
 |
(39)
|
Jos riippumattomat muuttujat 
, 
, …, 
on Poisson-jakauma parametreilla 
, 
, …, 
ja sitten
 |
(40)
|
: lla on Poisson-jakauma parametrilla
 |
(41)
|
Tämä näkyy, koska kumulanttigeneraatiofunktio on
 |
(42)
|
 |
(43)
|
Saslaw (1989) on käyttänyt Poisson-jakauman yleistystä mallintamiseen havaittu galaksien ryhmittyminen maailmankaikkeudessa. Tämän jakelun muodon antaa
 |
(44)
|
missä 
on galaksien määrä tilavuudessa 
, 
, 
on galaksien keskimääräinen tiheys ja 
, jossa 
on painovoiman ja kineettisen suhteen suhde omituisten liikkeiden energia, 
antaa
 |
(45)
|
joka on todellakin Poisson-jakauma ja 
. Vastaavasti 
antaa 
.