Pinta-alan laskeminen
Pinta-alan laskeminen
Pinta-ala mitataan neliöinä (tai neliöyksikköinä).
Kuinka monta neliötä tässä suorakulmiossa on?

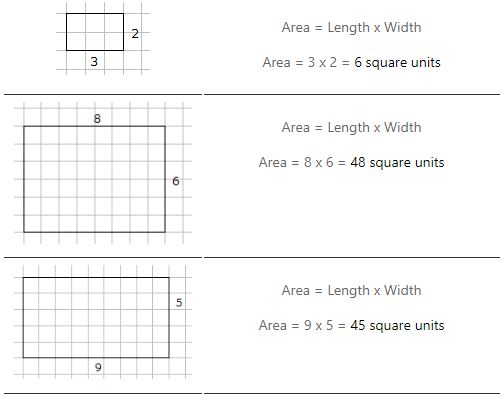
Voimme laskea neliöt tai voimme ota pituus ja leveys ja käytä kertolaskua. Yllä olevan suorakulmion pinta-ala on 15 neliöyksikköä.
Suorakulmion pinta-ala on = pituus x leveys
Esimerkkejä suorakulmion pinta-alan laskemisesta
Alueen mittausyksiköt
Mittaamme alueen käyttämällä neliöitä. Käytämme erikokoisia neliöitä sen mukaan, kuinka suuri tai pieni alue on.
| Esimerkki | Ruudun sivun pituus | Yksikkö |
| Ruudun koko naulaa peukalolle | millimetri | mm2 |
| paperin koko | senttimetri | cm2 |
| Huoneen koko | Mittari | m2 |
| Kaupungin koko | Kilometri | km2 |
Älä unohda pikkuista
Kirjoitamme neliökoot pienellä 2 yksikön viereen.
Kirjoitamme mm2, cm2, m2, km2, cm2
Voimme sanoa ”63 millimetriä neliössä” tai ”63 neliömetriä”
Voimme käyttää pieniä neliöitä suurten pinta-alojen mittaamiseen. Ainoa ongelma tässä on, että joudumme käyttämään erittäin suuria numerot. Esimerkiksi kentän suuruus voi olla 5 000 000 000 neliömetriä, kun 5 000 neliömetriä olisi paljon helpompi sanoa, kirjoittaa ja visualisoida.
Kuulet todennäköisesti enemmän yksiköitä alueen mittaamiseksi; neliötuumaa, neliöjalkaa, neliömetriä, neliökilometriä, hehtaaria, hehtaaria ovat kaikki yksiköitä, joita käytetään alueen mittaamiseen.
Lisää esimerkkejä alueen laskemisesta
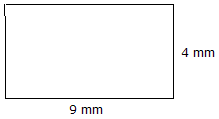 |
Pinta-ala = Pituus x leveys Pinta-ala = 9 mm x 4 mm = 36 mm2 |
 |
Pinta-ala = Pituus x leveys Pinta-ala = 7 cm x 6 cm = 42 cm2 |
 |
Pinta-ala = Pituus x Leveys Pinta-ala = 8 mx 2 m = 16 m2 |
 |
Alue = Pituus x Leveys Pinta-ala = 7 km x 5 km = 35 km2 |
Neliön pinta-ala
Neliön pituus ja leveys ovat samat, joten meidän on vain kerrottava pituus pituudella.
| Pinta-ala = Pituus x Pituus Pinta-ala = 6 cm x 6 cm = 36 cm2 |
Ympyrän alue
Ympyrän pinta-ala = πr2
missä r on ympyrän säde ja π on ympyrän kehän suhde sen halkaisijaan.
π (lausutaan ”piirakaksi” ja kirjoitetaan usein ”Pi”) on ääretön desimaali, jolla on yhteinen arvion 3,14159. Lisätietoja Pi: stä saat täältä
Esimerkki ympyrän pinta-alan laskemisesta
 |
Area = πr2 Alue = 3.14159 x (4 cm) 2 Pinta-ala = 3,14159 x 16 cm2 Pinta-ala = 50,27 cm2 Vastaus pyöristetään kahden desimaalin tarkkuudella |
Selitys ympyräkaavan alueelle
Ota ympyrä ja jaa se yhtä suurikokoisiin sektoreihin ja järjestä ne uudelleen alla olevan kuvan mukaisesti. Huomaa, kuinka kun sektorit pienenevät, muodosta tulee enemmän suorakulmion muotoinen. Huomaa: Ei ole mitään rajoitusta sille, kuinka pienet nämä sektorit voivat olla ja kuinka läheisesti ne voivat muistuttaa suorakulmiota järjestyksessä.
Oletetaan, että tiedämme, että ympyrän ympärysmitta on 2πr, voimme lisätä ulottuvuuksia ”suorakulmio” alla olevan kuvan mukaisesti. Käyttämällä suorakulmion pinta-alan kaavan aluetta, alue = leveys x korkeus, voimme nähdä, kuinka suorakulmiona uudelleen määritetyn ympyrämme voidaan näyttää olevan pinta-ala, joka on likimääräinen πr xr tai πr2
Ympyrä Sektorit järjestetty uudelleen

Ympyrän sektorit järjestetty uudelleen – käynnistys näyttää suorakulmiolta

Alue Yhdistelmämuodot
Monissa tapauksissa kokonaispinta-alan laskeminen edellyttää useamman kuin yhden alueen laskemista, jota seuraa joko yhteenlasku, vähennyslasku tai jokin muu toimintojen yhdistelmä tarvittavan alueen löytämiseksi.
Huomaa: Alla olevissa esimerkeissä mittayksiköitä ei näytetä, ja vastaukset ja π (Pi) arvo on pyöristetty lähimpään sadasosaan.
Esimerkki: Yksinkertaiset yhdistelmämuodot
Alla oleva esimerkki pinta-alan laskemisesta on suhteellisen yksinkertainen. Muoto voidaan nähdä kolmiona, joka on yhdistetty suorakulmioon.
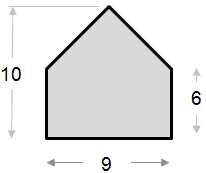 |
Kolmion osan alue: ½ x pohja x korkeus ½ x 9 x 4 = 18 Suorakulmion osan alue: Kokonaispinta-ala = 18 + 54 = 72 |
Yllä oleva esimerkki kuvaa yleistä vaatimusta työskenneltäessä yhdisteen kanssa muodot – sellaisten mittojen löytäminen, joita ei näytetä. Kun opetat lapsiasi, anna tarvittaessa apua näiden ”puuttuvien” ulottuvuuksien löytämiseksi. Alla on toinen esimerkki.
Mittojen etsiminen
 |
Mitkä ovat pienen suorakulmaisen osan mitat? Leveys? 12 – 7 – 2 = 3 Korkeus? 8-6 = 2 |
Esimerkki: Alueen vähentäminen toisesta
Alla olevassa esimerkissä muoto voidaan nähdä suorakulmiona, jossa on leikattu kolmio.
 |
Suorakulmion osan alue: leveys x korkeus 5 x 6 = 30 Kolmion osan alue: Kokonaispinta-ala = 30 – 4,50 = 25,50 |
Esimerkki: Osittaiset alueet
Alla oleva esimerkki on samanlainen kuin yllä, vaikka koska meillä on puoliympyrä, meidän on laskettava murtoluku (puolet) Huomaa tässä esimerkissä halkaisija eikä säde.
 |
Kolmion osan alue: ½ x pohja x korkeus ½ x 6 x 6 = 18 Puoliympyrän osan alue: Kokonaispinta-ala = 18 – 3,53 = 14,47 |
Esimerkki: Päätökset! Yhdistää? Vähennä
On tavallista, että lopullinen pinta-ala lasketaan useammalla kuin yhdellä tavalla. Alla olevissa esimerkeissä muoto voidaan nähdä kahtena suorakulmiona yhdistettynä tai yhtenä suurena suorakulmiona, jossa on pienempi suorakulmio ”leikattu” oikeasta yläkulmasta.
Alueen laskentataulukoiden laskeminen
Tulosta esitä alla luetellut laskentataulukot ja käytä niitä harjoitellessasi lapsia ohjataessasi.
- Alueiden – suorakulmioiden ja neliöiden laskeminen
- Alueiden – suorakulmioiden laskeminen
- Laskeminen Alueet – suorakulmiot
- Yhdiste-alueiden laskeminen esim suorakulmaisilla muotoilla
- Yhdistealueiden laskeminen esim. suorakulmioilla, kolmioilla ja ympyröillä
- Alueiden laskeminen esim. kolmioista
- Ympyrän alue
- Pinta-alojen laskeminen esim. suorakulmaisesta prismasta
Löydät lisää tulostettavia geometrian laskentataulukoita täältä.