Mittaus: Alueiden kaavojen löytäminen

Aluekaavat

Opiskelijat, joilla on epävirallinen käsitys siitä, että alue on 2-D Alueen sisällä olevat ”tavarat” voivat keksiä itselleen suurimman osan kaavoista, joita heiltä usein pyydetään vain muistaa. Jokainen kaava, jonka he keksivät uudelleen, vahvistaa heidän ymmärrystään (ja muistia) muista tuntemistaan kaavoista. (Katso myös pinta-ala.)

Suorakulmioiden pinta-ala

Valitsemalla neliö pinta-alayksiköksi saamme intuitiivisen kuvan suorakulmioiden pinta-alasta. Jos päätämme, että tämän neliön pinta-ala on 1, seitsemän kertaa pidemmän suorakulmion 7 × 1 kuin sen pinta-ala.

Suorakulmion, joka on kaksinkertainen -korkeuteen, pinta-ala on kaksinkertainen, joten alueen on 2 × 7 pinta-alayksikköä. Voimme laskea seitsemän neliön kaksi riviä. Vastaavasti -laitteessa on 3 riviä 7 ruutua (tai 7 saraketta 3 neliötä), yhteensä 7 × 3 neliötä, joten sen pinta-ala on 21 neliöyksikköä.

Yhden rivin neliöiden määrä on suorakulmion pituus. Rivien lukumäärä on suorakulmion korkeus. Pinta-ala on siis pituus × korkeus.

Koska suorakulmio voidaan piirtää vinoon, ”korkeus” määritellään tarkoittamaan ”alustaan nähden kohtisuoraa suuntaa” ja ”pohja” määritellään olevan, hyvin, mitä puolta valitsetkin.

Se toimii numeroiden laskemisessa. Se toimii myös murtolukuissa. 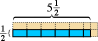Tässä esitetty sininen suorakulmio mittaa puolet Jos pituusyksikkö on korkea viisi ja puolet pituusyksikköä leveä. Jos valitsemme vastaavan neliön pinta-alayksiköksi, näemme, että sininen suorakulmio sisältää viisi puoliyksikköä pinta-alaa ja yhden neljänneksen pinta-alayksikköä tai kaksi ja kolme neljäsosaa pinta-alayksikköä. (Vaaleanpunaiset osat osoittavat jokaisen neliön pinta-alayksikön loppuunsaattamisen.)

Kaikkien numeroiden sisällyttämiseksi määritämme suorakulmion pinta-alaksi × korkeus (missä ”pohja” ja ”korkeus” tarkoittavat näiden sivujen pituutta mitattuna samoissa yksiköissä).

Suuntakulmien alue

Idean saaminen

Voimme selvittää kaavan yhdensuuntaisuuden pinta-alalle leikkaamalla suorakulmion tekeminen ja osien järjestäminen uudelleen suorakulmion muodostamiseksi. Koska suunta- ja suorakulmio koostuvat samoista osista, niillä on välttämättä sama alue. (Katso alueen määritelmästä lisätietoja siitä, miksi nämä alueet ovat samat.)

Voimme nähdä, että niillä on myös täsmälleen sama pohjan pituus (sininen) ja täsmälleen sama korkeus (vihreä). Koska pohja × korkeus antaa suorakulmion pinta-alan, voimme käyttää samoja mittoja suunnassa samankokoisina laskeaksesi sen pinta-alan: pohja × korkeus. (Kuten aikaisemmin, ”korkeus” mitataan kohtisuoraan alustaan nähden, ja ”pohja” on kumpi puoli valitaan ensin. Katso suunnassa.)

Edellä esitetyn leikkauksen avulla on helppo nähdä, että pohjan pituus on muuttumattomana. Itse asiassa kohtisuora leikkaus voidaan tehdä mistä tahansa pohjan pituudesta.

Reikien korottaminen

Intuitio ja todiste

Tämä leikkaus antaa intuitiivisen käsityksen rinnakkaispiirteen pinta-alan kaavasta, syyn siihen, että sen pitäisi olla sellainen kuin se on. Mutta emme ole kyseenalaistaneet, toimiiko dissektio todella ”.” Toisin sanoen, kun leikkaamme suunnan ja järjestämme sen osia uudelleen, odotamme saavan ja tulos näyttää varmasti tältä. esiintymät voivat olla harhaanjohtavia. Mikä vakuuttaa meille, että kun siirrämme kolmiota, tuloksena on suorakulmio? Entä jos se on enemmän kuin (joskin vähemmän liioiteltu)? Jos tulos ei ole aina täydellinen suorakulmio, emme voi käyttää tietämystämme suorakulmion pinta-alan kaavasta kehittääksesi kaavan suuntaissuunnalle. Lukiossa opiskelijat pystyvät todistamaan, että suorakulmion kaksi osaa muodostavat suorakulmion oikein koottuina . K-8-luokissa oppilaiden on pääosin luotettava visuaaliseen kokeiluun ja saatava intuitiivinen tunne. Lisätietoja miksi nämä leikkaukset toimivat.

Entä jos valitsemme pohjan lyhyen sivun?

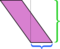
Voimme vapaasti valita minkä tahansa sivun pohjaksi; ”korkeus” on määritelty olevan mitattuna kohtisuoraan sivulle, jonka valitsemme pohjaksi. Jos otamme lyhyen sivun (sininen) pohjaksi, yllä esitetty leikkaus ei ole yhtä vakuuttava. Tämän korkeuden leikkaaminen ja osien järjestäminen jättää sotkua:

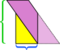
Tässä esimerkissä voimme pelastaa sotkun tekemällä vielä yhden leikkauksen, 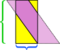, mutta entä jos rinnakkain olisi vielä pidempi ja laihempi?

On käynyt ilmi, että mikä tahansa suorakulmio, riippumatta siitä kuinka pitkä ja laiha, voidaan leikata tällä tavalla, jotta osat – ehkä monet niistä – voidaan järjestää uudelleen suorakulmioon. Mutta tarvitaan enemmän työtä sen osoittamiseksi, että tämä voidaan tehdä aina. Tarvitsemme toisen idean.

Hieman erilainen leikkausideo helpottaa elämää tässä tapauksessa. (Itse voit osoittaa, että se toimii myös alkuperäisessä tapauksessa.)

• Sulje suunnikkaan suorakulmioon.
• Suorakulmion kaksi osaa, jotka eivät ole suunnan sisällä, ovat yhtenevät kolmiot.
• Liuuta yhtä näistä kolmioista toisiaan kohti, kunnes ne kohtaavat suorakulmion. 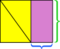Koska ulkopuolisen suorakulmion kokonaispinta-ala ei ole muuttunut (se on sama suorakulmio kuin aikaisemmin) ja keltainen alue ei ole muuttunut (palat vain liikkuivat ympäriinsä), niiden – violettien alueiden – on oltava samat. Kuten aiemmin, voimme myös nähdä, että suorakulmaisen purppuran alueen mitat ovat alkuperäisen suunnan perusta ja korkeus.

Intuitio ja todiste, nouse uudelleen : Jälleen leikkaus antaa olennaisen käsityksen, mutta se vie hieman enemmän työtä sen varmistamiseksi, että kaksi keltaista kolmiota, jotka näyttävät varmasti siltä kuin ne sopisivat yhteen suorakulmion muodostamiseksi, sopivat todella tarkalleen eikä vain melkein. p>

Miksi on tärkeää olla niin varovainen?

Kun rakennamme muita aluekaavoja (alla), haluamme käyttää tapaa löytää rinnakkaisen alueen alue, ja niin haluamme voidakseen luottaa löytämäämme sääntöön. Voimme olla varmoja siitä, että osien uudelleenjärjestäminen ei muuta aluetta: se on loppujen lopuksi se, miten määritämme alueen. Mutta meidän on myös oltava varmoja siitä, että osat sopivat yhteen tavallamme, tai me emme voi luottaa tekemiemme mittauksiin. Ja meidän on oltava varmoja siitä, että pohja × korkeus -sääntö ei riipu onnellisesta pohjan valinnasta.

Useimmilla opetussuunnitelmilla opiskelijoilla ei ole riittävän järjestelmällistä perustaa geometriseen tietoon ennen 8. luokkaa äänen todisteet siitä, että nämä leikkaukset toimivat. Mutta intuitiivinen ymmärrys riittää kaavojen selittämiseen ja perustelemiseen, ja hyvä perusta myöhemmälle geometriselle tutkimukselle.

Kolmion alue

Suuntaviivan alueen löytäminen auttaa meitä etsi kolmion pinta-ala.

Kolmion leikkaaminen

Voimme leikata kolmion kahteen osaan – yksi kolmio ja toinen puolisuunnikka – leikkaamalla sen yhdensuuntaiseksi tukikohtaan. Jos leikkaamme korkeuden tarkalleen kahtia tällä viipaleella, molemmat osat sopivat yhteen muodostaen suunnan, jolla on sama pohja mutta puolet korkeudesta.

Joten pohja × puolikorkeus antaa kolmion pinta-alan. Samanlainen leikkaus osoittaa puolen pohjan × korkeuden. Kumpi tahansa niistä pienenee arvoon bh.

Kolmion kaksinkertaistaminen ja tuloksena olevan alueen puolittaminen

Toinen ajattelutapa: kaksi kopiota kolmio muodostaa suunnan, jolla on sama pohja ja sama korkeus kuin kolmion kanssa.

Suuntaviivan pinta-ala on pohja × korkeus, mutta se on kaksinkertainen kolmion pinta-ala, joten kolmion pinta-ala on perusta × korkeus, kuten näimme leikkausmenetelmällä.

(Kuten aina , valitse ”pohja” ja mittaa korkeus kohtisuorassa pohjaan nähden vastakkaiseen kärkeen.)

Puolisuunnikkaan alue

Tuplaa kaksinkertaistetaan ja puolitetaan tuloksena oleva alue

Kuten kolmion kohdalla totta, kaksi puolisuunnikkaan kopiota voidaan sovittaa yhteen muodostamaan suunnaksi.

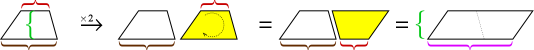
Suuntaviivan korkeus on sama kuin puolisuunnikkaan korkeus, mutta sen pohja on trapetsin kahden pohjan summa. Suorakulmion pinta-ala on siis korkeus × (pohja1 + pohja2). Mutta alue on kaksi puolisuunnikkaan muotoista, joten meidän on leikattava se kahtia, jotta saadaan puolisuunnikkaan pinta-ala.

Puolisuunnikkaan leikkaaminen

Voimme myös leikata trapetsin leikkaamalla tavalla. kolmio, jossa yksi viipale leikkaa sen korkeuden puoliksi. Nämä kaksi osaa sopivat yhteen ja muodostavat suunnan, jonka pohja on puolisuunnikkaan kahden pohjan summa, mutta jonka korkeus on puolet trapetsin korkeudesta.

Puolisuunnikkaan tapauksessa pohjat eivät voi valitaan haluamallaan tavalla. Kaksi yhdensuuntaista sivua ovat jalustoja, ja korkeus, kuten aina, on kohtisuora etäisyys yhdestä alustasta vastakkaiseen.

Tämän suunnan alue on sen korkeus (puolisuunnikkaan trapetsin korkeus) kertaa sen pohja (trapetsin pohjien summa), joten sen pinta-ala on puolikorkea × (pohja1 + pohja2). Koska suuntaussuunta on valmistettu täsmälleen samasta ”kamaa” kuin puolisuunnikkaan muotoinen, on myös trapetsin pinta-ala.

Kummassakin tapauksessa puolisuunnikkaan pinta-ala on × korkeus × (pohja1 + pohja2).

Muiden erityisten nelikulmioiden alue

Rombin alue

Rombin pinta-ala löytyy leikkaamalla ja järjestämällä palat suuntaussuunnan muodostamiseksi. Tämä voidaan tehdä useilla tavoilla:

1. Leikkaa lyhyemmän lävistäjän (a) yli muodostaaksesi kaksi yhtenevää kolmiota. Siirrä kolmion alaosaa ylemmän puoliskon viereen muodostaaksesi suunnan. Lyhyemmästä diagonaalista (a) tulee suunnan suunta, ja puolesta pidemmästä diagonaalista (b) tulee suunnan korkeus. Siten romun alue on * b tai diagonaalien tulo, joka on standardi kaava rombolle.
2. Toinen samanlainen tapa on leikata rombi neljään yhtenevään kolmioon ja järjestää ne uudelleen suorakulmioon, jonka pohja on lyhyempi ja puolet pidempi.
3. Leikkaamisen jälkeen rombin kahteen yhtenevään kolmioon, voimme laskea yhden kolmion pinta-alan, joka on * pohja (a) * korkeus ( b) = ab. Kerro sitten kahdella, koska niitä on kaksi: 2 * ab = ab.

Leijan alue

Leijan alue löytyy samanlaiselta kuin romun alue. Leikkaamalla pidemmästä diagonaalista saadaan kaksi yhtenevää kolmiota. Jos järjestämme ne uudelleen, voimme muodostaa suunnan, jossa pidempi lävistäjä (b) on pohja ja puolet lyhyempi lävistäjä (a) korkeus. Joten alueesta tulee b * a = ab. Monimutkaisempi lähestymistapa sisältää vähän algebraa. Leikkaa leija lyhyemmän lävistäjän yli muodostaaksesi kaksi kolmiota, joiden pohjana on lyhyempi lävistäjä (a). Ensimmäisen kolmion pinta-ala on siis a * squiggly, jossa squiggly on korkeus. Toisen kolmion alue on a * (b – squiggly), jossa (b – squiggly) on jäljellä oleva osa pidemmästä lävistäjästä. Kokonaispinta-alasta tulee siten ( a * squiggly) + ( a * (b – squiggly)). Vertailemalla a, meillä on a (squiggly + b – squiggly) = ab.

No, mitä tiedät. Periaatteessa sinun on tiedettävä vain suunnan suuntaisen kaavan alue ja sen jälkeen johdettava kaava muille.