Kuinka laskea tilavuus

Tilavuuden laskeminen

Tilavuus mitataan kuutioina (tai kuutioyksikköinä).

Kuinka monta kuutiota tässä suorakaiteen muotoisessa prismassa (neliönmuotoinen) on?

Voimme laskea kuutiot, vaikka pituuden, leveyden ja korkeuden ottaminen ja kertolasku on nopeampi. Yllä olevan suorakaiteen muotoisen prisman tilavuus on 48 kuutioyksikköä.

Suorakulmaisen prisman tilavuus on = pituus x leveys x korkeus

Esimerkkejä suorakulmion pinta-alan laskemisesta

Meidän on tehtävä kaksi kertolaskua äänenvoimakkuuden selvittämiseksi. Lasketaan yhden pinnan (tai sivun) pinta-ala ja kerrotaan se sen korkeudella. Alla olevat esimerkit osoittavat, kuinka tähän on kolme tapaa.

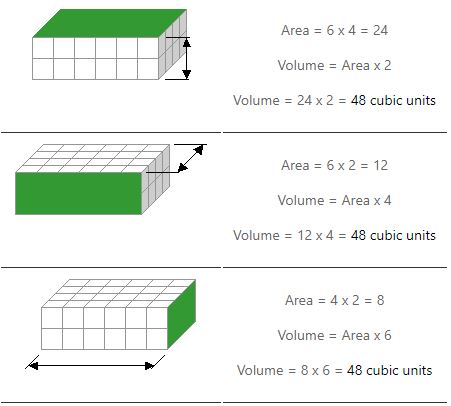
Huomaa, kuinka saamme saman vastauksen riippumatta siitä, mitä puolta käytämme alueen löytämiseen.

Kun lapsesi alkaa työskennellä alueen ja kehän kanssa, hän työskentelee yleensä kahdella ulottuvuudella – neliöt, suorakulmiot, kolmiot jne., jotka näytetään paperilla tasaisina – syvyyttä tai 3. ulottuvuutta ei ole. Työskentely äänenvoimakkuuden kanssa sisältää 3 ulottuvuutta. Varmista, että lapsesi on tietoinen tästä eikä ajattele kuutioita ja muita paperilla näytettyjä 3D-muotoja olevan vain toinen ”sivun muoto”. Näytä heille todellisia laatikoita ja osoita, kuinka ne voidaan piirtää (tai esittää) kaksiulotteiselle paperille. Toisin sanoen, varmista, että paperilla olevien ja tosielämässä olevien välillä on yhteys.

Varmista, että lapsesi ei hämmenty äänenvoimakkuuden käytöstä, jota käytetään puhuttaessa äänekkyydestä. .

Mittayksiköt

Mittayksiköiden välillä on hyvin suuria eroja. Esimerkiksi metrissä on 100 senttimetriä, mutta 1 000 000 (kyllä, 1 miljoonaa) ) kuutiosenttimetriä kuutiometrissä.

Miksi suuri ero? Koska tilavuudessa meillä ei ole vain pituutta, meillä on pituus, leveys ja korkeus. Alla oleva sokerikuutioesimerkki osoittaa tämän.

Kuinka paljon sokeria? 1 m3 tai 1 000 000 cm3

Ajattele täyttää erittäin iso laatikko (se olisi 1 metriä leveä, 1 metri pitkä, yksi metri korkea) sokerikuutioilla (jokaisen kanssa 1 senttimetri).

	Vaihe 1: yksi rivi laatikon alaosaa pitkin – joka olisi 100 sokerikuutiot
	Vaihe 2: peitä loput laatikon pohjat – joka antaisi yhteensä 100 riviä kullekin 100 sokerikuutiota. 100 x 100 = 10000 sokeria kuutiota ison laatikon alaosassa.
	Vaihe 3: Toista tätä 99 kertaa, kunnes 10000 kuution kerrokset pinottu 100 syvälle. 10000 x 100 = 1 000 000 sokerikuutioita

1 m3 on 1 000 000 cm3 – varo, ettei sokeria ole liikaa!

Tilavuuden mittaamiseen on muitakin yksiköitä; kuutiometriä, kuutiometriä, kuutiometriä ovat kaikki yksiköitä, joita käytetään tilavuuden mittaamiseen. Millilitraa, litraa, gallonaa käytetään myös erityisesti nesteitä mitattaessa.

Älä unohda pikku 3

Kirjoitamme kuutiokoot käyttämällä pieniä 3 yksikön vieressä.
Kirjoitamme mm3, cm3, m3, km3, cm3
Voimme sanoa ”85 senttimetriä kuutioina” tai ”85 kuutiosenttimetriä”

Esimerkkejä suorakulmaisten prismojen tilavuuden laskemisesta

	Äänenvoimakkuus = Pituus x Leveys x Korkeus Tilavuus = 12 cm x 8 cm x 6 cm = 576 cm3
	Tilavuus = Pituus x Leveys x Korkeus Tilavuus = 20 mx 2 mx 2 m = 80 m3
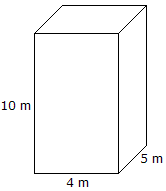	Tilavuus = Pituus x Leveys x Korkeus Tilavuus = 10 mx 4 mx 5 m = 200 m3

Sylinterin tilavuus

Sylinterin tilavuuden laskeminen der tarkoittaa alustan pinta-alan kertomista sylinterin korkeudella. Sylinterin pohja on pyöreä ja ympyrän pinta-alan kaava on: ympyrän pinta-ala = πr2. Ympyrän alueella on enemmän.

Tilavuus = Pohjan pinta-ala x korkeus Äänenvoimakkuus = πr2 xh Tilavuus = πr2 h

Huomaa: alla olevissa esimerkeissä käytämme arvoa 3,14 arvoksi π (Pi): lle.

Esimerkki sylinterin tilavuuden laskemisesta

Mitat ovat cm.

Tilavuus = πr2 h Tilavuus = 3.14 x 3 x 3 x 8 Tilavuus = 226,08 cm3

Kartion tilavuus

Kartion tilavuus on yhtä kolmasosa sylinterin tilavuudesta, jonka korkeus ja pohjan pinta-ala vastaavat. Tämä antaa käyrän tilavuuden kaavan alla olevan kuvan mukaisesti.

Volume = 1/3 πr2h

Esimerkki kartion tilavuuden laskemisesta

Mitat ovat cm.

Tilavuus = 1/3 πr2 h Tilavuus = 1/3 x 3,14 x 2 x 2 x 7 Tilavuus = 29,31 cm3

Pallon tilavuus

Pallon tilavuuden kaava on esitetty alla.

Volume = 4/3 πr3

Esimerkki pallon tilavuuden laskemisesta

Mitat ovat cm.

Volume = 4/3 πr3 Volume = 4/3 x 3,14 x 4 x 4 x 4 Tilavuus = 267,95 cm3

Tulostettavat volyymitaulukot

Käytä laskentataulukkoa harjoitellaksesi volyymien laskemista.

• Volyymin etsiminen kuutioyksikköinä – suorakaiteen muotoiset prismat ja komposiitit
• Suorakulmaisten prismojen määrät
• Suorakulmaisten prismojen määrät
• ”Reaalimaailman” esineiden määrät esim. viljalaatikoista
• Tilavuuksien laskeminen esim. kolmiomaisia prismoja ja sylintereitä

Täältä löydät muita geometrian laskentataulukoita kehältä, alueelta ja muulta.