Eksponentiaalijakauma
kirjoittanut tohtori Marco Taboga
Eksponentiaalijakauma on jatkuva todennäköisyysjakauma, jota käytetään mallinnetaan aika, jonka meidän on odotettava ennen tietyn tapahtuman tapahtumista. Se on geometrisen jakauman jatkuva vastine, joka on sen sijaan erillinen.
Joskus sitä kutsutaan myös negatiiviseksi eksponentiaalijakaumaksi.
Johdanto
Kuinka paljon aikaa kuluu ennen maanjäristystä tietyllä alueella? Kuinka kauan meidän on odotettava, kunnes asiakas tulee myymäläämme? Kuinka kauan kestää, ennen kuin puhelukeskus vastaanottaa seuraavan puhelun? Kuinka kauan kone toimii rikkoutumatta?
Tällaisiin kysymyksiin vastataan usein todennäköisyysperusteisesti käyttämällä eksponentiaalijakaumaa.
Kaikki nämä kysymykset koskevat tarvitsemaamme aikaa odottaa ennen tietyn tapahtuman tapahtumista. Jos tätä odotusaikaa ei tunneta, on usein tarkoituksenmukaista ajatella sitä satunnaismuuttujana, jolla on eksponentiaalijakauma.
Karkeasti sanottuna tarvitsemme aikaa 
odottaa ennen tapahtuman esiintymistä on eksponentiaalijakauma, jos todennäköisyys, että tapahtuma tapahtuu tietyllä aikavälillä, on verrannollinen kyseisen aikavälin pituuteen.
Tarkemmin sanottuna : llä on eksponentiaalijakauma, jos ehdollinen todennäköisyys on suunnilleen verrannollinen ajanjaksojen pituuteen ja , milloin tahansa hetkessä .
Monissa käytännön tilanteissa tämä ominaisuus on hyvin realistinen. Tästä syystä eksponentiaalijakaumaa käytetään niin laajalti odotusaikojen mallintamiseen.
Eksponenttijakauma liittyy tiukasti Poisson-jakaumaan. Jos 1) tapahtuma voi tapahtua useammin kuin kerran ja 2) kahden peräkkäisen tapahtuman välillä kulunut aika on eksponentiaalisesti jakautunut ja riippumaton aikaisemmista tapahtumista, niin tapahtuman tapahtumien määrällä tietyllä aikayksiköllä on Poisson-jakauma. Kutsumme lukijan tutustumaan Poisson-jakauman luentoon saadaksesi yksityiskohtaisemman selityksen ja intuitiivisen graafisen esityksen tästä tosiasiasta.
Määritelmä
Eksponentiaalijakaumalle on ominaista seuraava.
Määritelmä Olkoon jatkuva satunnaismuuttuja. Olkoon sen tuki positiivisten reaalilukujen joukko: Olkoon . Sanomme, että : llä on eksponentiaalijakauma parametrilla vain ja vain, jos sen todennäköisyystiheysfunktio on Parametria kutsutaan nopeusparametriksi.
Satunnaismuuttujaa, jolla on eksponentiaalijakauma, kutsutaan myös eksponentiaaliseksi satunnaismuuttujaksi.
Seuraava on osoitus siitä, että on oikeutettu todennäköisyystiheysfunktio.
Negatiivisuus on ilmeistä. Meidän on osoitettava, että : n integraali : n kanssa on yhtä suuri kuin . Tämä todistetaan seuraavasti:
Eksponentiaalijakauman ymmärtämiseksi paremmin voit tarkastella sen tiheyskaavioita.
Nopeusparametri ja sen tulkinta
Olemme maininneet, että todennäköisyys, että tapahtuma tapahtuu kahden päivämäärän ja on verrannollinen arvoon (riippuu tiedoista, joita ei ole tapahtunut ennen ). Nopeusparametri on suhteellisuusvakio: missä on ääretön pienin arvo korkeampi kuin (eli funktio , joka menee nollaan nopeammin kuin tekee).
Yllä oleva suhteellisuusehto riittää myös kuvaamaan eksponentiaalijakaumaa täysin.
Ehdotus Suhteellisuusehto on tyytyväinen vain, jos : llä on eksponentiaalijakauma.
Ehdollinen todennäköisyys voidaan kirjoittaa muodossa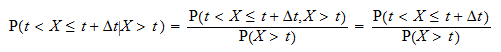 
Merkitään nimellä : n jakelutoiminto, eli ja sen selviytymistoiminto: Sitten Jakamalla molemmat puolet , saadaan missä on määrä, joka pyrkii kun on taipumus . Ottaen rajoja molemmille puolille, saamme tai johdannaisen määritelmän mukaan: Tämä differentiaaliyhtälö voidaan ratkaista helposti ketjulla sääntö: Kun otamme integraalin arvosta molempien osapuolten , saamme ja tai Mutta (koska ei voi ottaa negatiivisia arvoja) merkitsee molempien osapuolten eksponentointia, saadaan Siksi tai Mutta tiheysfunktio on ensimmäinen jakelutoiminnon johdannainen: ja oikeanpuoleisin termi on eksponentiaalisen satunnaismuuttujan tiheys. Siksi suhteellisuusvaatimus täyttyy vain, jos on eksponentiaalinen satunnaismuuttuja
Odotettu arvo
Eksponentiaalisen satunnaismuuttujan odotettu arvo on
Se voidaan johtaa seuraavasti: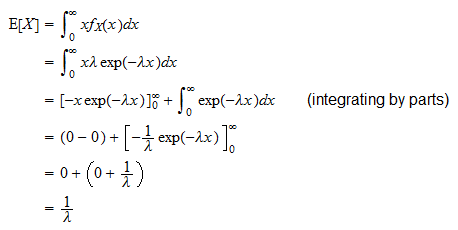 
Varianssi
Varianssi eksponentiaalinen satunnaismuuttuja on
Se voidaan johtaa tavallisen varianssikaavan () ansiosta: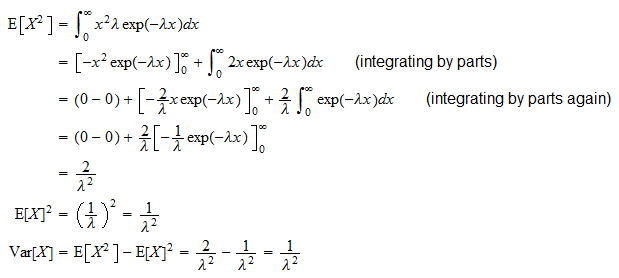 
Hetken luontitoiminto
Eksponentiaalisen satunnaismuuttujan hetkenmuodostustoiminto on määritetty kaikille :
Hetkenmuodostustoiminnon määritelmä antaa Of tietenkin yllä olevat integraalit yhtyvät vain, jos , ts. vain jos . Siksi eksponentiaalisen satunnaismuuttujan momenttia tuottava funktio on olemassa kaikille .
Luonteenomainen funktio
Eksponentiaalisen satunnaismuuttujan ominaisuusfunktio on
Käyttämällä ominaisfunktion määritelmää ja sitä, että voimme kirjoittaa Laskemme nyt kaksi integraalia erikseen . Ensimmäinen integraali on 
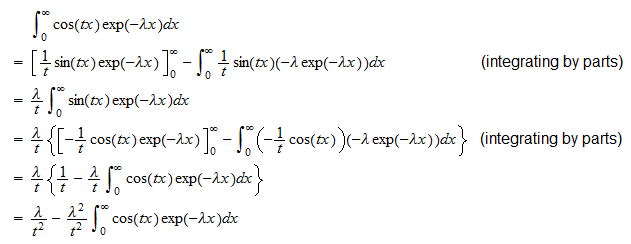Siksi , joka voidaan järjestää uudelleen tuottamaan tai Toinen integraali on 
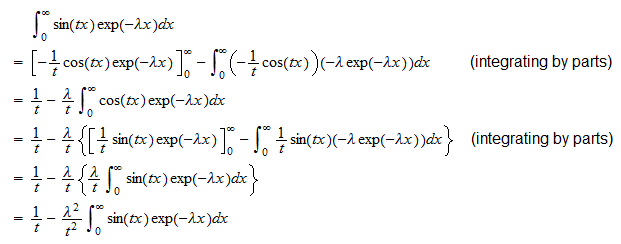Siksi , joka voidaan järjestää uudelleen tuottamaan tai Laittamalla palat yhteen saamme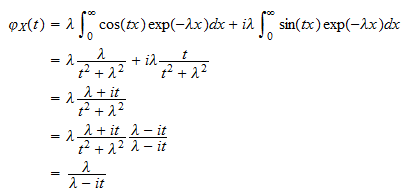 
Jakamistoiminto
Eksponentiaalisen satunnaismuuttujan jakelutoiminto on
Jos , niin koska ei voi ottaa negatiivisia arvoja. Jos , niin
Lisätietoja
Seuraavista osioista löydät lisätietoja eksponentiaalijakaumasta.
Muistiton ominaisuus
Yksi eksponentiaalijakauman tärkeimmistä ominaisuuksista on muistiton ominaisuus: mille tahansa .
Tämä osoitetaan seuraavasti: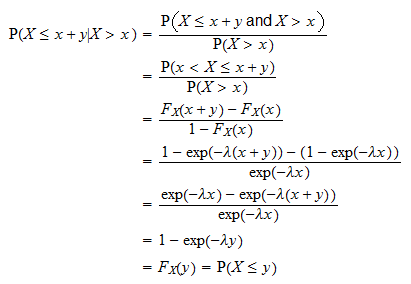 
on aika, jonka meidän on odotettava ennen tiettyä tapahtumaa tapahtuu. Yllä oleva ominaisuus sanoo, että todennäköisyys, että tapahtuma tapahtuu pituuden aikana, on riippumaton siitä, kuinka paljon aikaa on jo kulunut () ilman tapahtumaa.
Eksponentiaalisten satunnaismuuttujien summa on gamma-satunnaismuuttuja
Oletetaan, että , , …, ovat keskenään riippumattomia satunnaismuuttujia, joilla on eksponentiaalijakauma parametrilla .
Määritä
Sitten summa on gamma-satunnaismuuttuja parametreillä ja .
Tämä on osoitettu momentilla generoivat funktiot (muista, että keskenään riippumattomien satunnaismuuttujien summan hetkenmuodostustoiminto on vain niiden momenttia generoivien funktioiden tulo): Jälkimmäinen on gamman hetken tuottava funktio jakelu parametreilla ja . Joten : llä on gammajakauma, koska kahdella satunnaismuuttujalla on sama jakauma, kun niillä on sama hetken tuottava funktio.
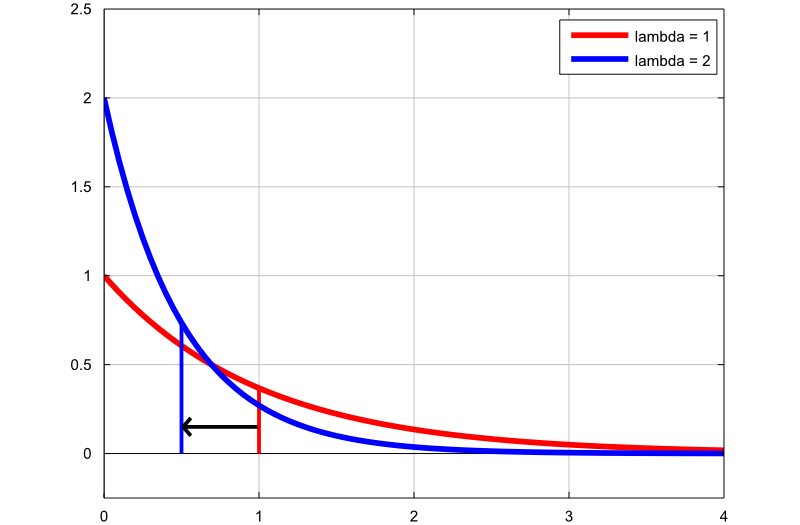
Satunnaismuuttujalla sanotaan joskus olevan myös Erlang-jakauma. Erlang-jakauma on vain erityinen tapaus Gamma-jakaumasta: Gamma-satunnaismuuttuja on myös Erlang-satunnaismuuttuja, kun se voidaan kirjoittaa eksponentiaalisten satunnaismuuttujien summana. p> Seuraava käyrä näyttää kuinka eksponentiaalijakauman tiheys muuttuu muuttamalla nopeusparametriä:
-
ensimmäinen kaavio (punainen viiva) on eksponentiaalisen satunnaismuuttujan todennäköisyystoiminto nopeusparametrilla
; -
toinen kaavio (sininen viiva) on eksponentiaalisen satunnaismuuttujan todennäköisyystiheysfunktio, jonka nopeusparametri on
.
Ohut pystysuora viiva osoittaa kahden jakauman keskiarvon. Huomaa, että suurentamalla nopeusparametriä laskemme jakauman keskiarvon arvosta arvoon .
Ratkaistut harjoitukset
Alla on joitain harjoituksia selitetyillä ratkaisuilla.
Harjoitus 1
Olkoon eksponentiaalinen satunnaismuuttuja parametrilla . Laske seuraava todennäköisyys:
Ensinnäkin voimme kirjoittaa todennäköisyyden muodossa käyttämällä sitä, että todennäköisyys, että jatkuva satunnaismuuttuja saa minkä tahansa tietyn arvon, on nolla (katso Jatkuvat satunnaismuuttujat ja nollatodennäköisyystapahtumat). Todennäköisyys voidaan nyt kirjoittaa -funktion muodossa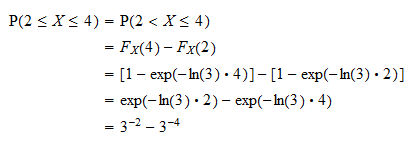 
Harjoitus 2
Oletetaan, että satunnaismuuttujalla on eksponentiaalijakauma parametrilla . Laske seuraava todennäköisyys:
Tämä todennäköisyys voidaan helposti laskea käyttämällä :
Harjoitus 3
Mikä on todennäköisyys, että satunnaismuuttuja on pienempi kuin odotettu arvo, jos : llä on eksponentiaalijakauma parametrilla ?
Eksponentiaalisen satunnaismuuttujan parametri on odotettavissa oleva arvo Yllä oleva todennäköisyys voidaan laskea käyttämällä :
Lainaus
Mainitse nimellä: