College Algebra (Suomi)
Oppimistulokset
- Tunnista parabolan kärkipiste, symmetria-akseli, y-leikkaus ja pienin tai suurin arvo se on kaavio.
- Tunnista toissijainen funktio, joka on kirjoitettu yleisesti ja kärkipisteessä.
- Määritä neliöllinen funktio yleisessä muodossa, kärkipiste.
- Määritä toimialue ja toissijaisen funktion alue tunnistamalla kärkipiste maksimin tai minimin arvoksi.
Neliöllisen funktion kaavio on U-muotoinen käyrä, jota kutsutaan parabolaksi. Yksi kaavion tärkeä piirre on, että sillä on äärimmäinen piste, jota kutsutaan kärjeksi. Jos parabolia avautuu, kärki edustaa kaavion alinta pistettä tai neliöfunktion pienintä arvoa. Jos paraboli avautuu alas, kärki edustaa kaavion korkeinta pistettä tai enimmäisarvoa. Kummassakin tapauksessa kärkipiste on kaavion käännekohta. Graafi on myös symmetrinen kärkipisteen läpi vedetyn pystysuoran viivan kanssa, jota kutsutaan symmetriakseliksi.
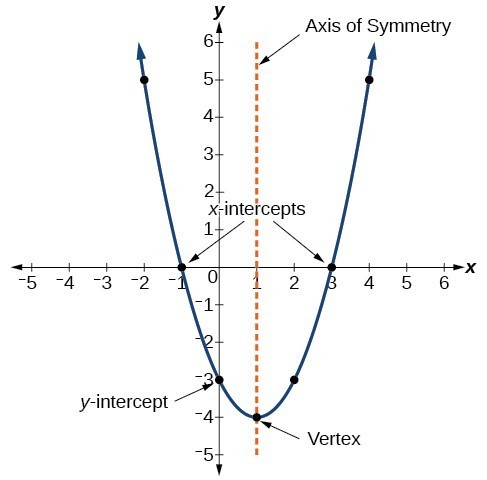
Toissijaisten funktioiden yhtälöt
Neliöllisen funktion yleinen muoto esittää funktion muodossa
f \ left (x \ right) = a {x} ^ {2} + bx + c
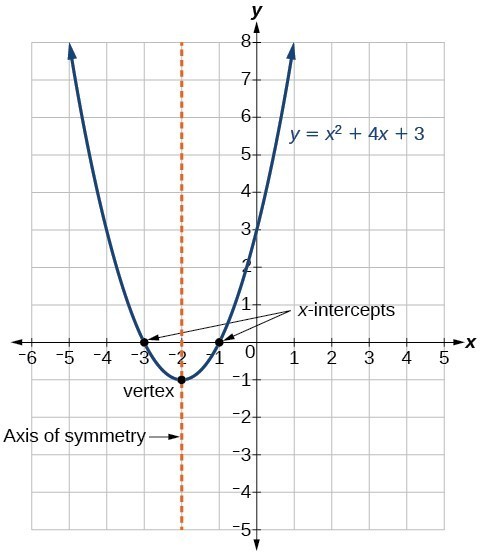
Sijoitusfunktion vakiomuoto esittää funktion muodossa
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Annetaan yleensä neliöfunktio muodossa, etsi parabolin kärki.
Yksi syy, miksi haluamme ehkä tunnistaa parabolin kärjen, on se, että tämä piste ilmoittaa meille, missä lähdön suurin tai pienin arvo esiintyy, k ja missä se tapahtuu, h. Jos meille annetaan toisen asteen funktion yleinen muoto:
f (x) = ax ^ 2 + bx + c
Voimme määritellä kärki (h, k) seuraavasti:
Neliöfunktion toimialueen ja alueen etsiminen
Mikä tahansa numero voi olla neliöfunktion syötearvo. Siksi minkä tahansa toissijaisen funktion toimialue on kaikki reaaliluvut. Koska paraboloilla on maksimissaan tai minimissään kärki, alue on rajoitettu. Koska parabolan kärkipiste on joko suurin tai pienin, alue koostuu kaikista y-arvoista, jotka ovat suurempia tai yhtä suuria kuin kärkipisteen y-koordinaatit tai pienemmät tai yhtä suuret kuin y-koordinaatit käännekohdassa , riippuen siitä, avautuuko vai jatkuuko paraboli.
Osallistu!
Paranna tätä sivuaLisätietoja