Tunnista pystysuora ja vaakasuora oireet College Algebra

marraskuu 8, 2020

College Algebra (Suomi)

Tarkastelemalla järkevän funktion kaaviota voimme tutkia sen paikallista käyttäytymistä ja nähdä helposti, onko asymptooteja. Voimme jopa pystyä arvioimaan heidän sijaintinsa. Jopa ilman kaaviota voimme silti määrittää, onko tietyllä rationaalisella funktiolla mitään asymptooteja, ja laskea niiden sijainnin.

Pystysuorat asymptootit

Rationaalisen funktion pystysuuntaiset oireet voivat olla löytyi tutkimalla nimittäjän tekijöitä, jotka eivät ole yhteisiä osoittajan tekijöille. Pystysuuntaisia oireettomia esiintyy tällaisten tekijöiden nollissa.

Ohjeet: Kun annat järkevän funktion, tunnista kaikki sen kuvaajan pystysuorat oireet.

Kerro osoitin ja nimittäjä.
Huomaa kaikki rajoitukset toiminnon toimialueella.
Vähennä lauseketta peruuttamalla yleisimmät tekijät osoittajassa ja nimittäjässä.
Huomaa kaikki arvot jotka aiheuttavat nimittäjän nollaksi tässä yksinkertaistetussa versiossa. Täällä esiintyy pystysuoria oireettomia.
Huomaa kaikki rajoitukset verkkotunnuksessa, jossa oireita ei esiinny. Nämä ovat irrotettavia epäjatkuvuuksia.

Irrotettavat epäjatkuvuudet

Toisinaan kaavio sisältää reiän: yhden pisteen, jossa kuvaajaa ei ole määritelty, osoittaa avoin ympyrä. Kutsumme tällaista reikää irrotettavaksi epäjatkuvuudeksi.

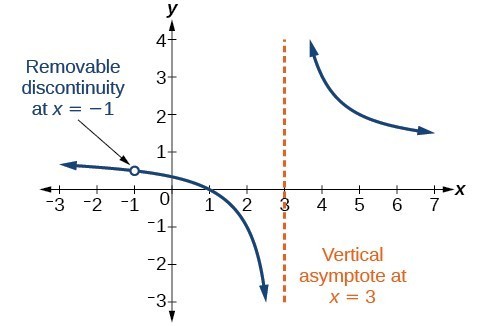
f \ left (x \ right) = \ frac {\ left (x + 1 \ right) \ left (x – 1 \ oikea)} {\ vasen (x + 1 \ oikea) \ vasen (x – 3 \ oikea)}

Kuva 10

Yleinen huomautus: Rationaalisten toimintojen irrotettavat epäjatkuvuudet

Rationaalisen funktion kaaviossa esiintyy irrotettava epäjatkuvuus kohdassa x = a, jos a on nolla nimittäjän kertoimelle, joka on yhteinen osoittajan tekijän kanssa. Me laskemme laskurin ja nimittäjän ja tarkistamme yhteiset tekijät. Jos löydämme sellaista, asetamme yhteisen kertoimen arvoksi 0 ja ratkaisemme. Tämä on irrotettavan epäjatkuvuuden sijainti. Tämä pätee, jos tämän tekijän moninaisuus on suurempi tai yhtä suuri kuin nimittäjässä. Jos tämän tekijän moninaisuus on nimittäjässä suurempi, siinä arvossa on edelleen asymptootti.

Vaaka-asymptootit

Vaikka pystysuorat asymptootit kuvaavat kuvaajan tuloksen ollessa erittäin suuri tai hyvin pieni, vaakasuorat asymptootit auttavat kuvaamaan kuvaajan käyttäytymistä, kun tulo kasvaa hyvin suureksi tai hyvin pieneksi. Muistakaa, että polynomin loppukäyttäytyminen heijastaa päätermin käyttäytymistä. Samoin järkevä funktion loppukäyttäytyminen heijastaa osoittaja- ja nimittäjäfunktioiden etusuhteiden suhdetta.

Vaakasuuntaisten asymptoottien tarkistuksessa on kolme erillistä tulosta:

Tapaus 1: Jos nimittäjän aste > osoittajan aste, y = 0: lla on vaakasuora asymptootti.

\ text {Esimerkki:} f \ left (x \ right) = \ frac {4x + 2} {{x} ^ {2} + 4x – 5}

Tapaus 2: Jos nimittäjän aste < osoittajan aste yhdellä, saamme vinon asymptootin.

\ text {Esimerkki:} f \ vasen (x \ oikea) = \ frac {3 {x} ^ {2} -2x + 1} {x – 1}

\ text {Esimerkki:} f \ vasen (x \ oikea) = \ frac {3 {x} ^ {2} +2} {{x} ^ {2 } + 4x – 5}

Huomaa, että vaikka rationaalisen funktion kaavio ei koskaan ylitä pystysuoraa asymptoottia, kaavio voi tai ei saa ylittää vaakasuoraa tai vino asymptootti. Lisäksi, vaikka rationaalisen funktion kaaviossa voi olla monia pystysuoria asymptooteja, kaaviossa on enintään yksi vaakasuora (tai vino) asymptootti.

On huomattava, että jos osoittajan aste on suurempi kuin nimittäjän aste useammalla kuin yhdellä, kaavion loppukäyttäytyminen jäljittelee pienennetyn loppukäyttäytymisfraktion käyttäytymistä. Jos meillä olisi esimerkiksi toiminto

f \ left (x \ right) = \ frac {3 {x} ^ {5} – {x} ^ { 2}} {x + 3}

loppukäyttäytymisellä

f \ vasen (x \ oikea) \ approx \ frac {3 {x } ^ {5}} {x} = 3 {x} ^ {4},

kaavion loppukäyttäytyminen näyttäisi samanlaiselta kuin tasaisen polynomin, jolla on positiivinen johtokerroin.

x \ \ \ \ \ infty, f \ left (x \ right) \ to \ infty

A Yleinen huomautus: Rationaaliset toiminnot

Rationaalisen funktion vaakasuora asymptootti voidaan määrittää katsomalla osoittajan ja nimittäjän astetta.

Osoittimen aste on pienempi kuin nimittäjän aste: vaakasuora asymptootti kohdassa y = 0.
Osoittimen aste on yhtä suuri kuin nimittäjän aste: ei vaakasuoraa asymptoottia; kalteva asymptootti.
Osoittimen aste on yhtä suuri kuin nimittäjän aste: vaakasuora asymptootti johtavien kertoimien suhteen.

Yleinen huomautus: Rationaalisten funktioiden sieppaukset

Rationaalisella funktiolla on y-leikkaus, kun tulo on nolla, jos toiminto on määritetty nollaksi. Rationaalisella funktiolla ei ole y-leikkausta, jos funktiota ei ole määritelty nollassa.

Samoin järkevällä funktiolla on x-sieppauksia tuloissa, jotka aiheuttavat lähdön nollan. Koska murtoluku on vain yhtä suuri kuin nolla, kun osoittaja on nolla, x-sieppauksia voi esiintyä vain, kun järkevän funktion osoittaja on nolla.

Kokeile 7

Kun otetaan huomioon vastavuoroinen neliöfunktio, joka on siirretty oikealle 3 yksikköä ja alaspäin 4 yksikköä, kirjoita tämä järkeväksi funktioksi. Etsi sitten x- ja y-sieppaukset sekä vaaka- ja pystysuuntaiset asymptootit.

Ratkaisu

admin