BFS vs. DFS: Tiedä ero

mikä on BFS ?

BFS on algoritmi, jota käytetään tietojen piirtämiseen tai puuhakuun tai kulkeviin rakenteisiin. Algoritmi vierailee ja merkitsee tehokkaasti kaikki kaavion avainsolmut tarkasti leveydeltään.

Tämä algoritmi valitsee kaaviosta yhden solmun (alku- tai lähdekohdan) ja vierailee sitten kaikki valitun solmun vieressä olevat solmut. Kun algoritmi vierailee ja merkitsee aloitussolmun, se siirtyy kohti lähimpiä avaamattomia solmuja ja analysoi ne.

Kun olet käynyt, kaikki solmut on merkitty. Nämä iteraatiot jatkuvat, kunnes kaavion kaikki solmut on vierailtu ja merkitty onnistuneesti. BFS: n koko muoto on leveyshaku.

Tässä BSF vs. DFS-binaaripuun opetusohjelma, opit:

• Mikä on BFS?
• Mikä on DFS?
• Esimerkki BFS: stä
• Esimerkki DFS: stä
• Ero BFS: n ja DFS-binääripuun välillä
• BFS: n sovellukset
• DFS: n sovellukset

Mikä on DFS?

DFS on algoritmi graafien tai puiden etsimiseen tai kulkemiseen syvyyssuunnassa. Algoritmin toteutus alkaa juurisolmusta ja tutkii kutakin haaraa ennen paluuta. Se käyttää pinon tietorakennetta muistaa, saada seuraava kärki ja aloittaa haun aina, kun umpikuja esiintyy missä tahansa iteraatiossa. DFS: n koko muoto on syvyyshaku.

Esimerkki BFS: stä

Seuraavassa DFS-esimerkissä ovat käyttäneet kuvaajaa, jossa on 6 kärkeä.

Esimerkki BFS: stä

Vaihe 1)

Sinulla on kaavio seitsemästä luvusta välillä 0 – 6.

Vaihe 2)

0 tai nolla on merkitty juurisolmuksi.

Vaihe 3)

0 on käynyt, merkitty ja lisätään jonotietorakenteeseen.

Vaihe 4)

Jäljellä 0 vierekkäistä ja vierailematonta solmuissa käydään, merkitään ja lisätään jonoon.

Vaihe 5)

Liikkuvia iteraatioita toistetaan kaikissa solmuissa käydään.

Esimerkki DFS: stä

Seuraavassa DFS-esimerkissä olemme käyttäneet suuntaamatonta kuvaajaa, jossa on 5 kärkeä.

Vaihe 1)

Olemme aloittaneet kärjestä 0. Algoritmi alkaa asettamalla se vierailuluetteloon ja asettamalla kaikki sen vierekkäiset pisteet tietoihin rakenne, jota kutsutaan pinoksi.

Vaihe 2)

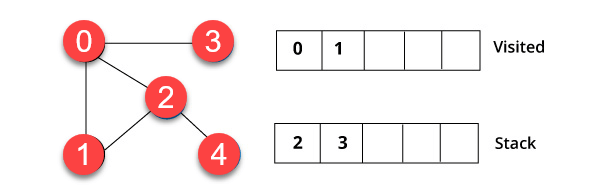
Vieraat elementissä , joka on pinon yläosassa, esimerkiksi, 1 ja mene sen vierekkäisiin solmuihin. Se johtuu siitä, että 0 on jo käynyt. Siksi käymme kärkipisteessä 2.

Vaihe 3)

Vertex 2: lla on vierailematon lähellä oleva kärkipiste 4. Siksi lisäämme sen pinoon ja vierailemme siinä.

Vaihe 4)

Lopuksi vierailemme viimeisessä kärjessä 3 siinä ei ole vierailemattomia vierekkäisiä solmuja. Olemme suorittaneet kaavion liikkumisen DFS-algoritmilla.

Ero BFS: n ja DFS-binaaripuun välillä

BFS	DFS
BFS löytää lyhimmän polun määränpäähän.	DFS menee osapuun alareunaan ja palaa sitten takaisin .
BFS: n koko muoto on Breadth-First Search.	DFS: n koko muoto on Depth First Search.
Se käyttää jonoa seuratakseen seuraavaa sijaintia.	Se seuraa pinoa seuraamaan seuraavaa sijaintia.
BFS kulkee puutason mukaan.	DFS kulkee puun syvyyden mukaan.
Se toteutetaan FI: n avulla FO-luettelo.	Se toteutetaan käyttämällä LIFO-luetteloa.
Se vaatii enemmän muistia verrattuna DFS: ään.	Se vaatii vähemmän muistia verrattuna BFS: ään.
Tämä algoritmi antaa matalin polun ratkaisun.	Tämä algoritmi ei takaa matalimman polun ratkaisua.
BFS: ssä ei tarvitse palata takaisin.	On tarve palata takaisin DFS: ään.
Et voi koskaan olla loukussa äärellisiin silmukoihin.	Voit olla loukussa äärettömiin silmukoihin.
Jos et löydä tavoitetta, sinun on ehkä laajennettava monia solmuja ennen ratkaisun löytämistä.	Jos et löydä tavoitetta, lehtisolmun takaisinkelaus voi esiintyä.

BFS: n sovellukset

Tässä ovat BFS: n sovellukset:

Painottamaton Kaaviot:

BFS-algoritmi voi helposti luoda lyhimmän polun ja pienimmän ulottuvuuspuun, jotta käy kaavion kaikki pisteet mahdollisimman lyhyessä ajassa erittäin tarkasti.

P2P-verkot:

BFS voidaan toteuttaa paikantamaan kaikki lähimmät tai vierekkäiset solmut vertaisverkossa. Tämä löytää tarvittavat tiedot nopeammin.

Verkkoindeksoijat:

Hakukoneet tai indeksointirobotit voivat helposti luoda useita hakemistotasoja käyttämällä BFS: ää. BFS-toteutus alkaa lähteestä, joka on verkkosivu, ja sitten se vierailee kaikki kyseisen lähteen linkit.

Verkon lähetys:

BFS-algoritmi ohjaa lähetettyä pakettia etsimään ja saavuttamaan kaikki solmut, joille se on osoitettu.

DFS: n sovellukset

Tässä ovat tärkeitä DFS: n sovelluksia:

Painotettu kaavio:

Painotetussa kaaviossa DFS-kaavion kulku luo lyhin polku ja vähintään ulottuva puu.

Syklin havaitseminen kaaviosta:

Kaaviossa on sykli, jos löysimme takareunan DFS: n aikana. Siksi meidän on suoritettava kaavion DFS ja tarkistettava takareunat.

Polun etsiminen:

Voimme erikoistua DFS-algoritmiin etsimään polkua kahden kärjen välillä.

Topologinen lajittelu:

Sitä käytetään ensisijaisesti töiden aikatauluttamiseen annetuista riippuvuuksista riippuen työpaikkaryhmästä. Tietojenkäsittelytieteessä sitä käytetään käskyjen ajoituksessa, tietojen sarjallisuudessa, logiikan synteesissä, kokoamistehtävien järjestyksen määrittämisessä.

Kaavion vahvasti yhdistettyjen komponenttien etsiminen:

Sitä käytetään DFS-kaaviossa, kun kaavion jokaisesta pisteestä on polku muihin jäljellä oleviin pisteisiin.

Palapelien ratkaiseminen vain yhdellä ratkaisulla:

DFS-algoritmi voidaan helposti mukauttaa etsimään kaikkia sokkelon ratkaisuja sisällyttämällä solmut vierailun kohteena olevaan joukkoon olemassa olevalle polulle.