Medición: Descubrir fórmulas para el área

Fórmulas para el área

Estudiantes que tienen la noción informal de que el área es la «cantidad de 2-D cosas ”contenidas dentro de una región pueden inventar por sí mismos la mayoría de las fórmulas que a menudo se les pide simplemente que memoricen. Cada fórmula que reinventan ayuda a fortalecer su comprensión (y memoria) de las otras fórmulas que conocen. (Véase también área de superficie.)

Área de rectángulos

Al elegir un cuadrado como unidad de área, obtenemos una idea intuitiva sobre el área de rectángulos. Si decidimos que el área de este cuadrado es 1, entonces un rectángulo que sea 7 veces más largo tendría 7 × 1 como su área.

Un rectángulo que tenga el doble de altura que tendría el doble de su área, por lo que el área de es 2 × 7 unidades de área. Podemos contar las dos filas de siete cuadrados. De manera similar, tiene 3 filas de 7 cuadrados (o 7 columnas de 3 cuadrados), para un total de 7 × 3 cuadrados, por lo que su área es de 21 unidades cuadradas.

El número de cuadrados en una fila es la longitud del rectángulo. El número de filas es la altura del rectángulo. Entonces, el área es longitud × altura.

Debido a que un rectángulo se puede dibujar inclinado, «altura» se define como «la dirección perpendicular a la base» y «base» se define como, bueno, sea cual sea el lado que elija.

Eso funciona para contar números. Incluso funciona para fracciones. 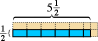El rectángulo azul que se muestra aquí mide la mitad unidad de longitud de alto por cinco unidades y media de longitud de ancho. Si elegimos el cuadrado correspondiente como nuestra unidad de área, vemos que el rectángulo azul contiene cinco medias unidades de área y un cuarto de unidad de área, o un total de dos y tres cuartos unidades de área. (Las partes rosadas muestran la terminación de cada unidad de área cuadrada).

Para incluir todos los números, definimos el área de un rectángulo como base × altura (donde «base» y «altura» significan las longitudes de esos lados, medidas en las mismas unidades).

Área de paralelogramos

Entendiendo la idea

Podemos encontrar una fórmula para el área de un paralelogramo diseccionando ing el paralelogramo y reorganizando las partes para hacer un rectángulo. Debido a que el paralelogramo y el rectángulo están compuestos por las mismas partes, necesariamente tienen la misma área. (Consulte la definición de área para obtener más información sobre por qué esas áreas son iguales).

Podemos ver que también tienen exactamente la misma longitud de base (azul) y exactamente la misma altura (verde). Debido a que la base × altura da el área del rectángulo, podemos usar las mismas medidas en el paralelogramo para calcular su área: base × altura. (Como antes, la «altura» se mide perpendicularmente a la base, y la «base» es el lado que elija primero. Vea el paralelogramo).

El corte que se muestra arriba hace que sea fácil ver que la longitud de la base es sin alterar. De hecho, el corte perpendicular se puede hacer en cualquier parte de la base.

Apuntalando los agujeros

Intuición y demostración

Esta disección da una comprensión intuitiva de la fórmula del área para un paralelogramo, una razón por la que debería ser lo que es. Pero no hemos cuestionado si la disección realmente «funciona». Es decir, cuando cortamos el paralelogramo y reorganizamos sus partes, esperamos obtener y el resultado ciertamente se ve así. Pero las apariencias pueden ser engañosas. ¿Qué nos asegura que cuando movemos ese triángulo, el resultado es un rectángulo? ¿Qué pasa si se parece más a (aunque menos exagerado)? Si el resultado no es siempre un rectángulo perfecto, no podemos usar nuestro conocimiento de la fórmula del área del rectángulo para desarrollar una fórmula para el paralelogramo. En la escuela secundaria, los estudiantes podrán demostrar que las dos partes del paralelogramo, cuando se vuelven a ensamblar correctamente, forman un rectángulo . En los grados K-8, en su mayor parte, los estudiantes deben confiar en el experimento visual y obtener una sensación intuitiva. Obtenga más información sobre por qué funcionan estas disecciones.

¿Qué pasa si elegimos el lado corto como base?

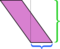
Somos libres de elegir cualquier lado como base; «altura» se define como medido perpendicular al lado que elegimos como base. Si tomamos el lado corto (azul) como base, la disección que se muestra arriba no es tan convincente. Cortar a lo largo de esa altitud y reorganizar las partes deja un desastre:

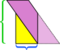
En este ejemplo en particular, podemos salvar el lío haciendo un corte más, 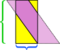pero ¿y si el paralelogramo fuera aún más largo y delgado?

Resulta que cualquier paralelogramo, no importa lo largo y delgado que sea, se puede diseccionar de esta manera para que las partes, quizás muchas de ellas, se puedan reorganizar en un rectángulo. Pero se necesita más trabajo para demostrar que esto siempre se puede hacer. Necesitamos otra idea.

Una idea de disección ligeramente diferente hace la vida mucho más fácil en este caso. (Por su cuenta, también puede demostrar que funciona en el caso original).

• Encierre el paralelogramo en un rectángulo.
• Las dos partes del rectángulo que no están dentro del paralelogramo son triángulos congruentes.
• Desliza uno de estos triángulos hacia el otro hasta que se junten para formar un rectángulo. 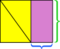Debido a que el área total del rectángulo exterior no ha cambiado (es el mismo rectángulo que antes) y el área amarilla no ha cambiado (las piezas se acaban de mover), la diferencia entre ellos, las áreas moradas, deben ser iguales. Como antes, también podemos ver que las dimensiones del área púrpura rectangular son la base y la altura del paralelogramo original.

Intuición y demostración, repita : Nuevamente, la disección proporciona la información esencial, pero se necesita un poco más de trabajo para asegurar que los dos triángulos amarillos, que ciertamente parecen encajar entre sí para formar un rectángulo, realmente encajan con precisión, y no solo casi.

¿Por qué es importante tener tanto cuidado?

Cuando construimos otras fórmulas de área (a continuación), querremos usar nuestro método de cómo encontrar el área de un paralelogramo, por lo que queremos para poder confiar en la regla que hemos encontrado. Podemos estar seguros de que reorganizar las partes no cambia el área: es decir, después de todo, cómo definimos el área. Pero también debemos asegurarnos de que las piezas encajen de la forma en que afirmamos que lo hacen, o no podemos confiar en las medidas que hemos realizado. Y debemos estar seguros de que la regla base × altura no depende de una elección afortunada de la base.

En la mayoría de los planes de estudio, los estudiantes no tienen una base suficientemente sistemática de conocimientos geométricos antes del octavo grado para hacer pruebas sólidas de que estas disecciones funcionan. Pero la comprensión intuitiva es suficiente para explicar y justificar las fórmulas, y una buena base para el estudio geométrico posterior.

Área del triángulo

Saber cómo encontrar el área de un paralelogramo nos ayuda encuentra el área de un triángulo.

Diseccionar el triángulo

Podemos diseccionar el triángulo en dos partes, una de ellas un triángulo y otra un trapezoide, cortándolo en paralelo a la base. Si cortamos la altura exactamente a la mitad con esa rebanada, las dos partes encajarán para formar un paralelogramo con la misma base pero la mitad de la altura.

Entonces, base × media altura da el área del triángulo. Una disección similar muestra media base × altura. Cualquiera de ellos se reduce a bh.

Duplicar el triángulo y luego dividir a la mitad el área resultante

Otra forma de pensar: dos copias de el triángulo forma un paralelogramo con la misma base y la misma altura que el triángulo.

El área del paralelogramo es base × altura, pero eso es el doble del área del triángulo, por lo que el área del triángulo es de base × altura, como vimos con el método de disección.

(Como siempre , elija una «base» y mida la altura perpendicular a esa base, desde la base hasta el vértice opuesto.)

Área del trapezoide

Duplicar el trapezoide y luego dividir a la mitad el área resultante

Como sucedió con el triángulo, dos copias de un trapezoide se pueden unir para formar un paralelogramo.

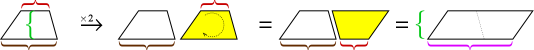
La altura del paralelogramo es la misma que la altura del trapezoide, pero su base es la suma de las dos bases del trapezoide. Entonces, el área del paralelogramo es la altura × (base1 + base2). Pero esa área son dos trapezoides, por lo que debemos cortarla por la mitad para obtener el área del trapezoide.

Diseccionar el trapezoide

También podríamos diseccionar el trapezoide de la forma en que diseccionamos el triángulo, con una sola rebanada que corta su altura a la mitad. Las dos partes encajan para formar un paralelogramo cuya base es la suma de las dos bases del trapezoide, pero cuya altura es la mitad de la altura del trapezoide.

En el caso del trapezoide, las bases no pueden ser elegido a voluntad. Los dos lados paralelos son las bases y la altura, como siempre, es la distancia perpendicular de una base a la opuesta.

El área de este paralelogramo es su altura (media altura del trapezoide) por su base (suma de las bases del trapezoide), por lo que su área es media altura × (base1 + base2). Debido a que el paralelogramo está hecho exactamente de la misma «materia» que el trapezoide, esa también es el área del trapezoide.

De cualquier manera, el área del trapezoide es × altura × (base1 + base2).

Área de otros cuadriláteros especiales

Área del rombo

El área de un rombo se puede encontrar cortando y reorganizando las piezas para formar un paralelogramo. Esto se puede hacer de varias maneras:

1. Corta la diagonal más corta (a) para formar dos triángulos congruentes. Mueva la mitad inferior del triángulo junto a la mitad superior para formar un paralelogramo. La diagonal más corta (a) se convierte en la base del paralelogramo y la mitad de la diagonal más larga (b) se convierte en la altura del paralelogramo. Por lo tanto, el área del rombo es a * b o el producto de las diagonales, que es la fórmula estándar para el rombo.
2. Otra forma similar es cortar el rombo en cuatro triángulos congruentes y reorganizarlos en un rectángulo con la diagonal más corta como base y la mitad de la diagonal más larga como altura.
3. Después de cortar el rombo en dos triángulos congruentes, podemos calcular el área de uno de los triángulos, que es * base (a) * altura ( b) = ab. Luego, multiplique por dos, ya que hay dos: 2 * ab = ab.

Área de la cometa

El área de una cometa se puede encontrar similar al área de un rombo. Cortar a lo largo de la diagonal más larga produce dos triángulos congruentes. Si los reorganizamos, podemos formar un paralelogramo con la diagonal más larga (b) como base y la mitad de la diagonal más corta (a) como la altura. Entonces, el área se convierte en b * a = ab. Un enfoque más complicado implica un poco de álgebra. Corta la cometa por la diagonal más corta para formar dos triángulos con la diagonal más corta (a) como base. Por lo tanto, el área del primer triángulo es a * ondulado, donde ondulado es la altura. El área del segundo triángulo es a * (b – ondulado), donde (b – ondulado) es la parte restante de la diagonal más larga. Por tanto, el área total se convierte en ( a * ondulado) + ( a * (b – ondulado)). Factorizando a, tenemos a (squiggly + b – squiggly) = ab.

Bueno, ¿qué sabes? Básicamente, solo necesita conocer la fórmula del área de un paralelogramo y luego derivar la fórmula de los demás.