Distribución exponencial
por Marco Taboga, PhD
La distribución exponencial es una distribución de probabilidad continua utilizada para Modele el tiempo que necesitamos esperar antes de que ocurra un evento determinado. Es la contraparte continua de la distribución geométrica, que en cambio es discreta.
A veces también se le llama distribución exponencial negativa.
Introducción
¿Cuánto tiempo pasará antes de que ocurra un terremoto en una región determinada? ¿Cuánto tiempo debemos esperar hasta que un cliente ingrese a nuestra tienda? ¿Cuánto tiempo pasará antes de que un centro de llamadas reciba la próxima llamada telefónica? ¿Cuánto tiempo funcionará una pieza de maquinaria sin romperse?
Preguntas como estas se responden con frecuencia en términos probabilísticos utilizando la distribución exponencial.
Todas estas preguntas se refieren al tiempo que necesitamos esperar antes de que ocurra un evento determinado. Si se desconoce este tiempo de espera, a menudo es apropiado pensar en él como una variable aleatoria que tiene una distribución exponencial.
En términos generales, el tiempo 
que necesitamos esperar antes de que ocurra un evento tiene una distribución exponencial si la probabilidad de que el evento ocurra durante un cierto intervalo de tiempo es proporcional a la duración de ese intervalo de tiempo.
Más precisamente, tiene una distribución exponencial si la probabilidad condicional es aproximadamente proporcional a la longitud del intervalo de tiempo comprendido entre los tiempos y , para cualquier instante de tiempo .
En muchas situaciones prácticas, esta propiedad es muy realista. Esta es la razón por la que la distribución exponencial se usa tanto para modelar los tiempos de espera.
La distribución exponencial está estrictamente relacionada con la distribución de Poisson. Si 1) un evento puede ocurrir más de una vez y 2) el tiempo transcurrido entre dos ocurrencias sucesivas se distribuye exponencialmente y es independiente de ocurrencias anteriores, entonces el número de ocurrencias del evento dentro de una unidad de tiempo dada tiene una distribución de Poisson. Invitamos al lector a ver la conferencia sobre la distribución de Poisson para una explicación más detallada y una representación gráfica intuitiva de este hecho.
Definición
La distribución exponencial se caracteriza de la siguiente manera.
Definición Sea una variable aleatoria continua. Sea su soporte el conjunto de números reales positivos: Sea . Decimos que tiene una distribución exponencial con el parámetro si y solo si su función de densidad de probabilidad es El parámetro se llama parámetro de tasa.
Una variable aleatoria que tiene una distribución exponencial también se denomina variable aleatoria exponencial.
La siguiente es una prueba de que es una función de densidad de probabilidad legítima.
La no negatividad es obvia. Necesitamos demostrar que la integral de sobre es igual a . Esto se demuestra de la siguiente manera:
Para comprender mejor la distribución exponencial, puede echar un vistazo a sus diagramas de densidad.
El parámetro de tasa y su interpretación
Hemos mencionado que la probabilidad de que el evento ocurra entre dos fechas y es proporcional a (condicional a la información de que no ha ocurrido antes del ). El parámetro de tasa es la constante de proporcionalidad: donde es un infinitesimal de orden superior a (es decir, una función de que llega a cero más rápidamente que hace).
La condición de proporcionalidad anterior también es suficiente para caracterizar completamente la distribución exponencial.
Proposición La condición de proporcionalidad se satisface solo si tiene una distribución exponencial.
La probabilidad condicional se puede escribir como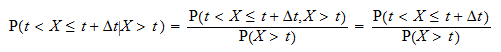 
Denote por la función de distribución de , es decir, y su función de supervivencia: Luego, Dividiendo ambos lados por , obtenemos donde es una cantidad que tiende a cuando tiende a . Tomando límites en ambos lados, obtenemos o, por la definición de derivada: Esta ecuación diferencial se resuelve fácilmente usando la cadena regla: Tomando la integral de a de ambos lados, obtenemos y o Pero (porque no puede tomar valores negativos) implica Al exponer ambos lados, obtenemos Por lo tanto, o Pero la función de densidad es la primera derivada de la función de distribución: y el término más a la derecha es la densidad de una variable aleatoria exponencial. Por lo tanto, la condición de proporcionalidad se cumple solo si es una variable aleatoria exponencial
Valor esperado
El valor esperado de una variable aleatoria exponencial es
Se puede derivar de la siguiente manera: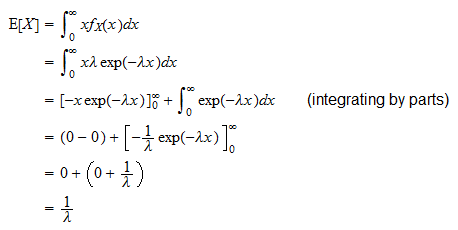 
Varianza
La varianza de una La variable aleatoria exponencial es
Es se puede derivar gracias a la fórmula de variación habitual (): 
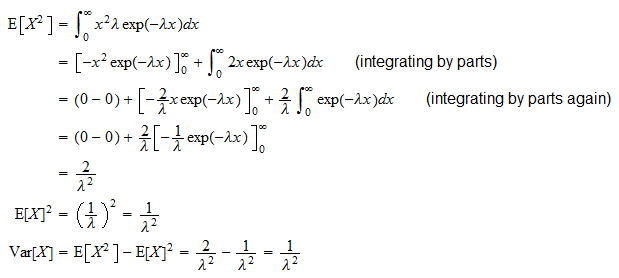
Función de generación de momento
La función de generación de momento de una variable aleatoria exponencial se define para cualquier :
La definición de función generadora de momentos da De Por supuesto, las integrales anteriores convergen solo si , es decir, solo si . Por lo tanto, la función de generación de momento de una variable aleatoria exponencial existe para todas las .
Función característica
La función característica de una variable aleatoria exponencial es
Al usar la definición de función característica y el hecho de que podemos escribir Ahora calculamos por separado las dos integrales . La primera integral es 
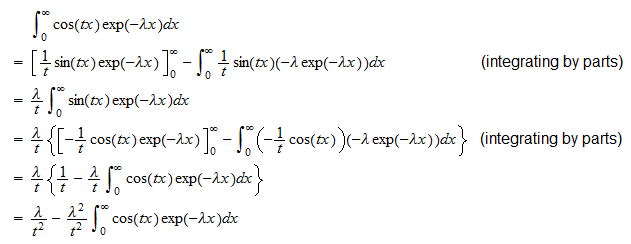Por lo tanto, que se puede reorganizar para producir o La segunda integral es 
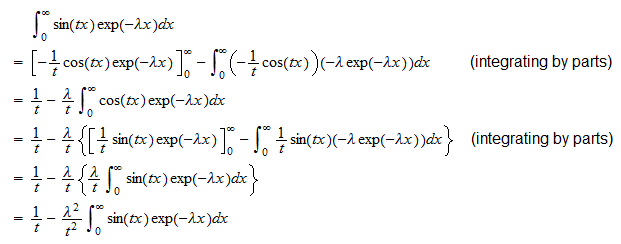Por lo tanto, que se puede reorganizar para producir o Al juntar las piezas, obtenemos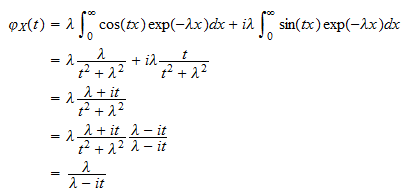 
Función de distribución
La función de distribución de una variable aleatoria exponencial es
Si , entonces porque no puede tomar valores negativos. Si , entonces
Más detalles
En las siguientes subsecciones puede encontrar más detalles sobre la distribución exponencial.
Propiedad sin memoria
Una de las propiedades más importantes de la distribución exponencial es la propiedad sin memoria: para cualquier .
Esto se demuestra de la siguiente manera: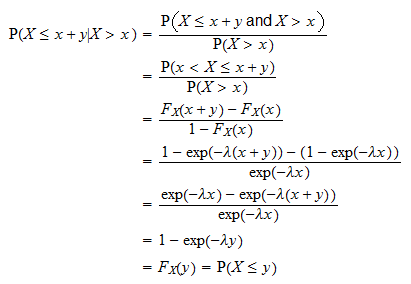 
es el tiempo que debemos esperar antes de un determinado evento ocurre. La propiedad anterior dice que la probabilidad de que el evento ocurra durante un intervalo de tiempo de duración es independiente de cuánto tiempo ya ha transcurrido () sin que suceda el evento.
La suma de las variables aleatorias exponenciales es una variable aleatoria Gamma
Supongamos , , …, son variables aleatorias mutuamente independientes que tienen una distribución exponencial con el parámetro .
Defina
Luego, la suma es una variable aleatoria Gamma con parámetros y .
Esto se prueba usando el momento funciones generadoras (recuerde que la función generadora de momentos de una suma de variables aleatorias independientes entre sí es solo el producto de sus funciones generadoras de momentos): Esta última es la función generadora de momentos de una Gamma distribución con los parámetros y . Entonces tiene una distribución Gamma, porque dos variables aleatorias tienen la misma distribución cuando tienen la misma función generadora de momentos.
A veces también se dice que la variable aleatoria tiene una distribución Erlang. La distribución de Erlang es solo un caso especial de la distribución Gamma: una variable aleatoria Gamma también es una variable aleatoria de Erlang cuando se puede escribir como una suma de variables aleatorias exponenciales.
Gráfica de densidad
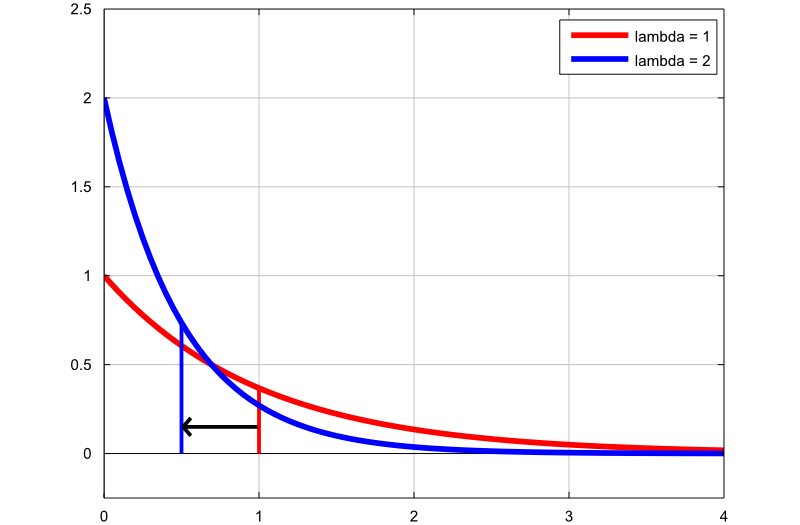
El siguiente gráfico muestra cómo cambia la densidad de la distribución exponencial al cambiar el parámetro de tasa:
-
el primer gráfico (línea roja) es la función de densidad de probabilidad de una variable aleatoria exponencial con parámetro de tasa
; -
el segundo gráfico (línea azul) es la función de densidad de probabilidad de una variable aleatoria exponencial con parámetro de tasa
.
Las líneas verticales finas indican las medias de las dos distribuciones. Tenga en cuenta que, al aumentar el parámetro de tasa, disminuimos la media de la distribución de a .
Ejercicios resueltos
A continuación puede encontrar algunos ejercicios con soluciones explicadas.
Ejercicio 1
Sea una variable aleatoria exponencial con el parámetro . Calcule la siguiente probabilidad:
En primer lugar, podemos escribir la probabilidad como utilizando el hecho de que la probabilidad de que una variable aleatoria continua tome cualquier valor específico es igual a cero (ver Variables aleatorias continuas y eventos de probabilidad cero) Ahora, la probabilidad se puede escribir en términos de la función de distribución de como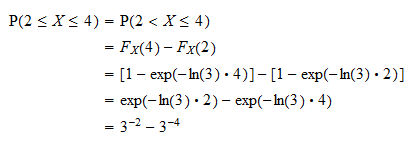 
Ejercicio 2
Suponga que la variable aleatoria tiene una distribución exponencial con el parámetro . Calcule la siguiente probabilidad:
Esta probabilidad se puede calcular fácilmente utilizando la función de distribución de :
Ejercicio 3
¿Cuál es la probabilidad de que una variable aleatoria es menor que su valor esperado, si tiene una distribución exponencial con el parámetro ?
El valor esperado de una variable aleatoria exponencial con parámetro es La probabilidad anterior se puede calcular utilizando la función de distribución de :
Cómo citar
Por favor, cite como: