Distribución de Poisson
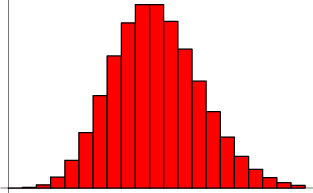
Dado un proceso de Poisson, la probabilidad de obtener exactamente 
éxitos en 
ensayos está dada por el límite de una distribución binomial
 |
(1)
|
Ver la distribución en función del número esperado de éxitos
 |
(2)
|
en lugar del tamaño de muestra 
para 
fijo, la ecuación (2) se convierte en
 |
(3)
|
Dejando que el tamaño de la muestra 
se vuelva grande, la distribución se acerca
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
que se conoce como distribución de Poisson (Papoulis 1984, págs. 101 y 554; Pfeiffer y Schum 1973, pág. 200). Tenga en cuenta que el tamaño de muestra 
se eliminó por completo de la función de probabilidad, que tiene la misma forma funcional para todos los valores de 
.
La distribución de Poisson se implementa en WolframLanguage como distribución de Poisson.
Como se esperaba, la distribución de Poisson se normaliza para que la suma de probabilidades sea igual a 1, ya que
 |
(9 )
|
La razón de probabilidades viene dada por
 |
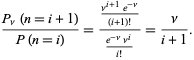(10)
|
La distribución de Poisson alcanza un máximo cuando
 |
(11)
|
donde es la constante de Euler-Mascheroni y 
es un número armónico, lo que lleva a la ecuación trascendental
 |
(12)
|
que no se puede resolver exactamente para 
.
La función generadora de momentos de la distribución de Poisson viene dada por
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
entonces
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, pág. 554).
Los momentos brutos también se pueden calcular directamente por suma, lo que produce una conexión inesperada con el polinomio Bell 
y los números de Stirling del segundo tipo,
 |
(21)
|
conocida como la fórmula de Dobiński.Por lo tanto,
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
Los momentos centrales se pueden calcular como
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
por lo que la media, la varianza, la asimetría y el exceso de curtosis son
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
La función característica para la distribución de Poisson es
(Papoulis 1984, págs. 154 y 554), y la función generadora de acumuladores es
 |
(34)
|
entonces
 |
(35)
|
La desviación media de la distribución de Poisson viene dada por
 |
(36)
|
La distribución de Poisson también se puede expresar en términos de
 |
(37)
|
 |
(38)
|
La función generadora de momentos de una distribución de Poisson en dos variables viene dada por
 |
(39)
|
Si las variables independientes 
, 
, …, 
tienen distribuciones de Poisson con parámetros 
, 
, …, 
, luego
 |
(40)
|
tiene una distribución de Poisson con parámetro
 |
(41)
|
Esto se puede ver ya que la función de generación acumulativa es
 |
(42)
|
 |
(43)
|
Saslaw (1989) ha utilizado una generalización de la distribución de Poisson para modelar el agrupamiento observado de galaxias en el universo. La forma de esta distribución viene dada por
 |
(44)
|
donde 
es el número de galaxias en un volumen 
, 
, 
es la densidad promedio de galaxias, y 
, con 
es la relación entre la energía gravitacional y la cinética energía de movimientos peculiares, dejando 
da
 |
(45)
|
que de hecho es una distribución de Poisson con 
. Del mismo modo, dejar 
da 
.