Cómo calcular el volumen

Cálculo del volumen

El volumen se mide en cubos (o unidades cúbicas).

¿Cuántos cubos hay en este prisma rectangular (cuboide)?

Podemos contar los cubos, aunque es más rápido tomar el largo, ancho y alto y usar la multiplicación. El prisma rectangular de arriba tiene un volumen de 48 unidades cúbicas.

El volumen de un prisma rectangular es = largo x ancho x alto

Ejemplos de cálculo del área de un rectángulo

Necesitamos hacer dos multiplicaciones para calcular el volumen. Calculamos el área de una cara (o lado) y lo multiplicamos por su altura. Los ejemplos siguientes muestran cómo hay tres formas de hacerlo.

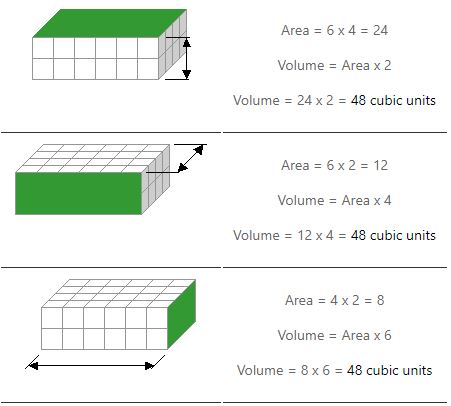
Observe cómo obtenemos la misma respuesta sin importar qué lado usemos para encontrar un área.

Cuando su hijo comience a trabajar con el área y el perímetro, generalmente trabajará con 2 dimensiones: cuadrados, rectángulos, triángulos, etc.que se muestran en el papel como planos; no hay profundidad ni tercera dimensión. Trabajar con volumen implica 3 dimensiones. Asegúrese de que su hijo sea consciente de esto y no piense en los cubos y otras formas 3D que se muestran en el papel como si fueran otra «forma en la página». Muéstreles cajas reales y muestre cómo se pueden dibujar (o representar) en una hoja de papel bidimensional. En otras palabras, asegúrese de que se establezca la conexión entre lo que está escrito en papel y lo que representa en el mundo real.

Asegúrese de que su hijo no se confunda con el uso del volumen como se usa cuando se habla de volumen .

Unidades para medir el volumen

Existen diferencias muy grandes entre las unidades de medida para el volumen. Por ejemplo, hay 100 centímetros en 1 metro pero hay 1,000,000 (sí, 1 millón ) centímetros cúbicos en un metro cúbico.

¿Por qué la gran diferencia? Porque en volumen no solo tenemos la longitud, tenemos la longitud, el ancho y la altura. El ejemplo de terrón de azúcar a continuación muestra esto.

¿Cuánto azúcar? 1 m3 o 1.000.000 cm3

Piense en llenar una caja muy grande (tendría 1 metro de ancho, 1 metro, largo y un metro de alto) con terrones de azúcar (con cada lado 1 centímetro).

	Paso 1: una fila en la parte inferior del cuadro – serían 100 terrones de azúcar
	Paso 2: cubra el resto de la base de la caja – eso daría un total de 100 filas cada una con 100 terrones de azúcar. 100 x 100 = 10,000 azúcares cubos en la parte inferior de la caja grande.
	Paso 3: Repite esto 99 veces hasta que haya capas de 10,000 cubos apilados 100 de profundidad. 10,000 x 100 = 1,000,000 cubos de azúcar

Hay 1,000,000 cm3 en 1 m3 – ¡tenga cuidado de no tener demasiada azúcar!

Hay otras unidades para medir el volumen; pulgadas cúbicas, pies cúbicos, yardas cúbicas son todas las unidades que se utilizan para medir el volumen. Los mililitros, litros y galones también se utilizan especialmente para medir líquidos.

No olvides los 3 pequeños

Escribimos tamaños cúbicos usando un pequeño 3 al lado de la unidad.
Escribimos mm3, cm3, m3, km3, cm3
Podemos decir «85 centímetros cúbicos» o «85 centímetros cúbicos»

Ejemplos de cálculo del volumen de prismas rectangulares

	Volumen = Largo x Ancho x Alto Volumen = 12 cm x 8 cm x 6 cm = 576 cm3
	Volumen = Largo x Ancho x Alto Volumen = 20 mx 2 mx 2 m = 80 m3
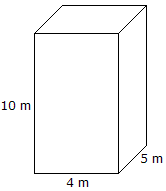	Volumen = Largo x Ancho x Altura volumen = 10 mx 4 mx 5 m = 200 m3

Volumen de un cilindro

Cálculo del volumen de un cilindro der implica multiplicar el área de la base por la altura del cilindro. La base de un cilindro es circular y la fórmula para el área de un círculo es: área de un círculo = πr2. Aquí hay más sobre el área de un círculo.

Volumen = Área de la base x Altura Volumen = πr2 xh Volumen = πr2 h

Nota: en los ejemplos siguientes usaremos 3.14 como valor aproximado para π (Pi).

Ejemplo de cálculo del volumen de un cilindro

Las dimensiones están en cm.

Volumen = πr2 h Volumen = 3.14 x 3 x 3 x 8 Volumen = 226.08 cm3

Volumen de un cono

El volumen de un cono es igual a un tercio del volumen de un cilindro con la misma altura y área de base. Esto da la fórmula para el volumen de un cono como se muestra a continuación.

Volumen = 1/3 πr2h

Ejemplo de cálculo del volumen de un cono

Las dimensiones están en cm.

Volumen = 1/3 πr2 h Volumen = 1/3 x 3,14 x 2 x 2 x 7 Volumen = 29,31 cm3

Volumen de una esfera

La fórmula para el volumen de una esfera se muestra a continuación.

Volumen = 4/3 πr3

Ejemplo de cálculo del volumen de una esfera

Las dimensiones están en cm.

Volumen = 4/3 πr3 Volumen = 4/3 x 3,14 x 4 x 4 x 4 Volumen = 267,95 cm3

Hojas de trabajo de volumen imprimibles

Utilice la hoja de trabajo a continuación para practicar el cálculo de volúmenes.

• Hallar el volumen en unidades cúbicas: prismas rectangulares y compuestos
• Volúmenes de prismas rectangulares
• Volúmenes de prismas rectangulares
• Volúmenes de objetos del «mundo real», p. ej. de cajas de cereales
• Cálculo de volúmenes, p. ej. de prismas triangulares y cilindros

Aquí obtendrá otras hojas de trabajo de geometría sobre perímetro, área y más.