Cómo calcular el área
Calcular el área
El área se mide en cuadrados (o unidades cuadradas).
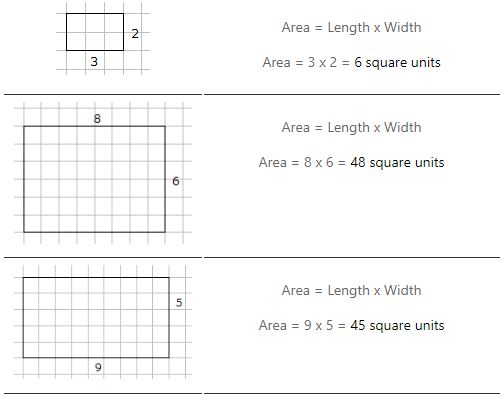
¿Cuántos cuadrados hay en este rectángulo?

Podemos contar los cuadrados o podemos toma el largo y el ancho y usa la multiplicación. El rectángulo de arriba tiene un área de 15 unidades cuadradas.
El área de un rectángulo es = largo x ancho
Ejemplos de cálculo del área de un rectángulo
Unidades para medir el área
Medimos el área usando cuadrados. Usamos diferentes tamaños de cuadrados según el tamaño del área.
| Ejemplo | Longitud del lado en cuadrados | Unidad |
| Tamaño del uña en el pulgar | Milímetro | mm2 |
| Tamaño de la hoja de papel | Centímetro | cm2 |
| Tamaño de una habitación | Metro | m2 |
| Tamaño de una ciudad | Kilómetro | km2 |
No olvides los 2 pequeños
Escribimos tamaños cuadrados usando un 2 pequeño al lado de la unidad.
Escribimos mm2, cm2, m2, km2, cm2
Podemos decir «63 milímetros cuadrados» o «63 milímetros cuadrados»
Podríamos usar cuadrados pequeños para medir áreas grandes. El único problema con esto es que terminaríamos teniendo que usar cuadrados muy grandes números. Por ejemplo, un campo podría medirse en 5.000.000.000 de milímetros cuadrados, cuando 5.000 metros cuadrados sería un tamaño mucho más fácil de decir, escribir y visualizar.
Probablemente oirá más unidades para medir el área; pulgadas cuadradas, pies cuadrados, yardas cuadradas, millas cuadradas, acres, hectáreas son todas las unidades utilizadas para medir el área.
Más ejemplos de cálculo de área
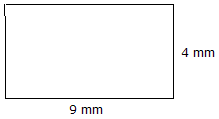 |
Área = Largo x Ancho Área = 9 mm x 4 mm = 36 mm2 |
 |
Área = Largo x Ancho Área = 7 cm x 6 cm = 42 cm2 |
 |
Área = Largo x Ancho Área = 8 mx 2 m = 16 m2 |
 |
Área = Longitud x Ancho Área = 7 km x 5 km = 35 km2 |
Área de un cuadrado
La longitud y el ancho de un cuadrado son iguales, por lo que solo necesitamos multiplicar la longitud por la longitud.
| Área = Longitud x Longitud Área = 6 cm x 6 cm = 36 cm2 |
Área de un círculo
El área de un círculo = πr2
donde r es el radio del círculo y π es la relación entre la circunferencia de un círculo y su diámetro.
π (pronunciado «pastel» y a menudo escrito «Pi») es un decimal infinito con un común aproximación de 3,14159. Puede encontrar más información sobre Pi aquí
Ejemplo de cálculo del área de un círculo
 |
Área = πr2 Área = 3.14159 x (4 cm) 2 Área = 3.14159 x 16 cm2 Área = 50.27 cm2 Respuesta redondeada a 2 decimales |
Explicación de la fórmula del área de un círculo
Tome un círculo y divídalo en sectores de igual tamaño y reorganícelos como se muestra a continuación. Observe cómo, a medida que los sectores se vuelven más pequeños, la forma se parece más a un rectángulo. Nota: No hay límite para cuán pequeños podrían ser estos sectores y cuán cerca podrían parecerse a un rectángulo cuando se organizan.
Suponiendo que sabemos que la circunferencia de un círculo es igual a 2πr, podemos agregar dimensiones a el «rectángulo» como se muestra a continuación. Usando la fórmula del área del área de un rectángulo, área = ancho x alto, podemos ver cómo nuestro círculo, reconfigurado como un rectángulo, puede mostrarse que tiene un área que se aproxima a πr xr o πr2
Círculo Sectores reorganizados

Sectores circulares reorganizados: inicio que parezca un rectángulo

Área de Formas compuestas
Hay muchos casos en los que el cálculo de un área total requiere que se calcule más de un área seguida de una suma, resta o alguna otra combinación de operaciones para encontrar el área requerida.
Nota: En los ejemplos siguientes, las unidades de medida no se muestran y las respuestas y el valor de π (Pi) se han redondeado a la centésima más cercana.
Ejemplo: Formas compuestas simples
El siguiente ejemplo de cálculo de área es relativamente simple. La forma se puede ver como un triángulo combinado con un rectángulo.
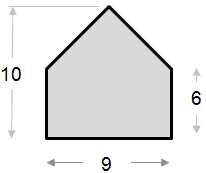 |
Área de la parte del triángulo: ½ x base x altura ½ x 9 x 4 = 18 Área de la parte rectangular: Área total = 18 + 54 = 72 |
El ejemplo anterior ilustra un requisito común cuando se trabaja con compuestos formas: encontrar dimensiones que no se muestran. Al dar clases particulares a sus hijos, ayude, cuando sea necesario, a encontrar estas dimensiones «faltantes». Hay otro ejemplo a continuación.
Encontrar las dimensiones
 |
¿Cuáles son las dimensiones de la parte rectangular pequeña? ¿Ancho? 12 – 7 – 2 = 3 ¿Altura? 8 – 6 = 2 |
Ejemplo: restar un área de otra
En el siguiente ejemplo, la forma se puede ver como un rectángulo con un triángulo cortado.
 |
Área de la parte del rectángulo: ancho x alto 5 x 6 = 30 Área de la parte del triángulo: Área total = 30 – 4.50 = 25.50 |
Ejemplo: áreas parciales
El siguiente ejemplo es similar al anterior, aunque, dado que tenemos un semicírculo, necesitamos calcular una fracción (la mitad) del área del círculo. Observe en este ejemplo el diámetro, no el radio.
 |
Área de la parte del triángulo: ½ x base x altura ½ x 6 x 6 = 18 Área de la parte del semicírculo: Área total = 18 – 3,53 = 14,47 |
Ejemplo: ¡Decisiones! ¿Combinar? Restar
Es común tener más de una forma de calcular el área final. En los ejemplos a continuación, la forma puede verse como dos rectángulos combinados o como un rectángulo grande con un rectángulo más pequeño «recortado» en la esquina superior derecha.
Calcular las hojas de trabajo del área
Imprimir Saque las hojas de trabajo que se enumeran a continuación y utilícelas para practicar al dar clases particulares a sus hijos.
- Cálculo de áreas: rectángulos y cuadrados
- Cálculo de áreas: rectángulos
- Cálculo Áreas: rectángulos
- Cálculo de áreas compuestas, p. Ej. con formas rectangulares
- Cálculo de áreas compuestas, p. ej. con rectángulos, triángulos y círculos
- Cálculo de áreas, p. ej. de triángulos
- Área de un círculo
- Calcular áreas de superficie, p. ej. de prismas rectangulares
Aquí encontrará más hojas de trabajo de geometría imprimibles.