Álgebra universitaria (Español)
Al observar la gráfica de una función racional, podemos investigar su comportamiento local y ver fácilmente si hay asíntotas. Incluso es posible que podamos aproximarnos a su ubicación. Sin embargo, incluso sin el gráfico, podemos determinar si una función racional dada tiene asíntotas y calcular su ubicación.
Asíntotas verticales
Las asíntotas verticales de una función racional pueden ser encontrado examinando los factores del denominador que no son comunes a los factores del numerador. Las asíntotas verticales ocurren en los ceros de dichos factores.
Cómo: Dada una función racional, identifica cualquier asíntota vertical de su gráfica.
- Factoriza el numerador y denominador.
- Tenga en cuenta las restricciones en el dominio de la función.
- Reduzca la expresión cancelando los factores comunes en el numerador y el denominador.
- Tenga en cuenta los valores que hacen que el denominador sea cero en esta versión simplificada. Aquí es donde ocurren las asíntotas verticales.
- Note cualquier restricción en el dominio donde no ocurren las asíntotas. Estas son discontinuidades removibles.
Discontinuidades removibles
Ocasionalmente, un gráfico contendrá un agujero: un solo punto donde el gráfico no está definido, indicado por un círculo abierto. Llamamos a ese agujero una discontinuidad removible.
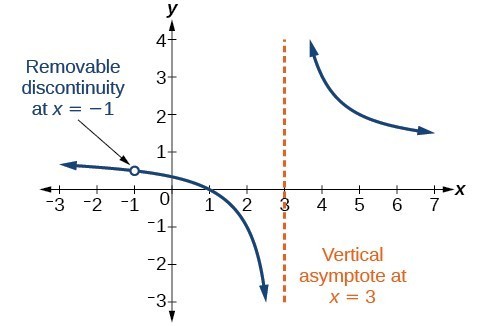
Figura 10
Una nota general: Discontinuidades removibles de funciones racionales
Una discontinuidad removible ocurre en el gráfico de una función racional en x = a si a es cero para un factor en el denominador que es común con un factor en el numerador. Factorizamos el numerador y el denominador y buscamos factores comunes. Si encontramos alguno, igualamos el factor común a 0 y resolvemos. Esta es la ubicación de la discontinuidad removible. Esto es cierto si la multiplicidad de este factor es mayor o igual que la del denominador. Si la multiplicidad de este factor es mayor en el denominador, entonces todavía hay una asíntota en ese valor.
Asíntotas horizontales
Mientras que las asíntotas verticales describen el comportamiento de una gráfico a medida que la salida se vuelve muy grande o muy pequeña, las asíntotas horizontales ayudan a describir el comportamiento de un gráfico cuando la entrada se vuelve muy grande o muy pequeña. Recuerde que el comportamiento final de un polinomio reflejará el del término principal. Del mismo modo, el comportamiento final de una función racional reflejará el de la razón de los términos principales de las funciones de numerador y denominador.
Hay tres resultados distintos al verificar las asíntotas horizontales:
Caso 1: si el grado del denominador > grado del numerador, hay una asíntota horizontal en y = 0.

Caso 2: Si el grado del denominador < grado del numerador en uno, obtenemos una asíntota inclinada.

Observe que, mientras que la gráfica de una función racional nunca cruzará una asíntota vertical, la El gráfico puede o no cruzar una horizontal o asíntota inclinada. Además, aunque la gráfica de una función racional puede tener muchas asíntotas verticales, la gráfica tendrá como máximo una asíntota horizontal (o inclinada).
Cabe señalar que, si el grado del numerador es mayor que el grado del denominador en más de uno, el comportamiento final del gráfico imitará el comportamiento de la fracción de comportamiento final reducido. Por ejemplo, si tuviéramos la función
con comportamiento final
el comportamiento final del gráfico sería similar al de un polinomio par con un coeficiente principal positivo.
Una nota general: asíntotas horizontales de Funciones racionales
La asíntota horizontal de una función racional se puede determinar observando los grados del numerador y el denominador.
- El grado del numerador es menor que el grado del denominador: asíntota horizontal en y = 0.
- El grado del numerador es mayor que el grado del denominador en uno: sin asíntota horizontal; asíntota inclinada.
- El grado del numerador es igual al grado del denominador: asíntota horizontal en la relación de los coeficientes principales.
Una nota general: intersecciones de funciones racionales
Una función racional tendrá una intersección en y cuando la entrada es cero, si el la función se define en cero. Una función racional no tendrá una intersección con el eje y si la función no está definida en cero.
Asimismo, una función racional tendrá intersecciones con el eje x en las entradas que hacen que la salida sea cero. Dado que una fracción solo es igual a cero cuando el numerador es cero, las intersecciones x solo pueden ocurrir cuando el numerador de la función racional es igual a cero.
Pruébelo 7
Dada la función recíproca al cuadrado que se desplaza hacia la derecha 3 unidades y hacia abajo 4 unidades, escribe esto como una función racional. Luego, encuentre las intersecciones en x e y y las asíntotas horizontal y vertical.
Solución